從圖來看反覆求Δx = - f(x1) / f'(x1) 並且依序找出 x1、x2、x3 在幾何上扮演什麼樣的意義。
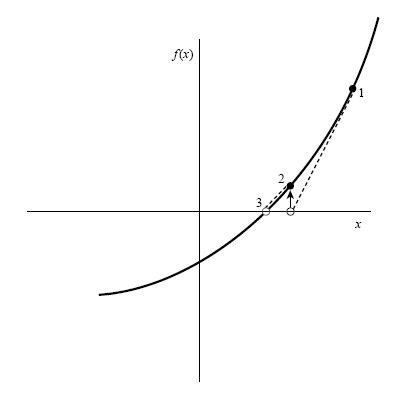
我們同時也要小心以下的狀況,
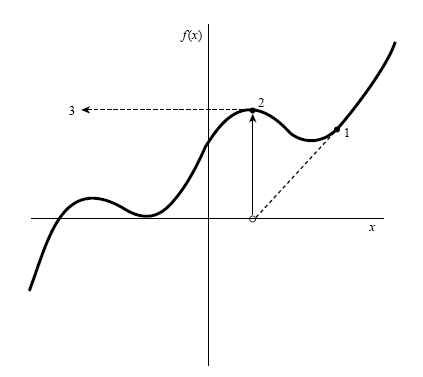
反映在公式中的,正是分母(斜率)不能為零的要求。
另外,還有收斂的過程卡在某一對點上,無法再進步。
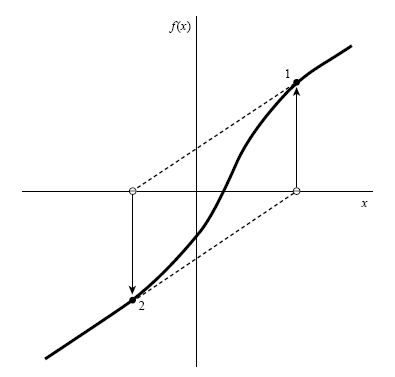
函數求根:牛頓法(含廣義牛頓法)
從公式來了解牛頓法
假設 x1 不是 f(x) 的根(因此 f(x1) 不等於 0),但也夠接近真正的根 x' 了。 假設還差 Δx (Δx = x' - x1),則寫下 f(x') 的泰勒展開會是
f(x1+Δx) = f(x1) + f'(x1)Δx + ...
忽略高次項,並用上 f(x') = 0(根的定義)
0 = f(x1) + f'(x1)Δx
Δx = - f(x1) / f'(x1)
這個Δx 的表示式是很有用的,它告訴我們,目前猜測的位置 x1 與根的位置大約還有 - f(x1) / f'(x1) 那麼遠。
有了這個資訊,我們當然就可以獲得更接近根的猜測值 x1 +Δx,在此可把它叫做是 x2。牛頓法就在這個簡單而有威力的演算法下,從 x1、x2、x3 一直更新下去,很快就找到函數根了。
(在不參考任何資料的情況下,要能推導出牛頓法的公式)
從圖形來了解牛頓法
從圖來看反覆求Δx = - f(x1) / f'(x1) 並且依序找出 x1、x2、x3 在幾何上扮演什麼樣的意義。
我們同時也要小心以下的狀況,
反映在公式中的,正是分母(斜率)不能為零的要求。
另外,還有收斂的過程卡在某一對點上,無法再進步。
函式 rtnewt
FUNCTION rtnewt(funcd,x1,x2,xacc)
INTEGER JMAX
REAL rtnewt,x1,x2,xacc
EXTERNAL funcd
PARAMETER (JMAX=20) Set to maximum number of iterations.
Using the Newton-Raphson method, find the root of a function known to lie in the interval
[x1, x2]. The root rtnewt will be refined until its accuracy is known within ±xacc. funcd
is a user-supplied subroutine that returns both the function value and the first derivative
of the function at the point x.
INTEGER j
REAL df,dx,f其中,使用者自己要給的副程式 funcd 是這樣被呼叫的

一個能使用 rtnewt 函式的主程式,其中並含要讓 rtnewt 呼叫的使用者提供之副程式 funcd (求函數 x3 的根), 請大家參考練習:
program rtnewt_main
real rtnewt, x1, x2, xacc
external rtnewt, funcdwrite (*,*) 'Please type in interval x1 and x2 :'
read (*,*) x1, x2
write(*,*) 'Please typle in theaccuracy for root finding :'
read (*,*) xacc
write(*,*) 'The root is ', rtnewt(funcd,x1,x2,xacc)
write(*,*) 'within the accuracy of +/- ', xacc
end
subroutine funcd(x,f,df)
real x, f, df
f = x**3
df = 3*(x**2)
end
函式 rtsafe
牛頓法雖然靠斜率的引導能很快地找到根,但也有前述幾種像是跑出範圍、走入無窮迴圈等狀況,純粹的牛頓法不一定能找到解。rtsafe 結合了快速牛頓法與穩定的二分法,在牛頓法失效的時候改用二分法,只要有包圍到根就一定會找得到。
FUNCTION rtsafe(funcd,x1,x2,xacc)
INTEGER MAXIT
REAL rtsafe,x1,x2,xacc
EXTERNAL funcd
PARAMETER (MAXIT=100) Maximum allowed number of iterations.
Using a combination of Newton-Raphson and bisection, find the root of a function bracketed
between x1 and x2. The root, returned as the function value rtsafe, will be refined until
its accuracy is known within ±xacc. funcd is a user-supplied subroutine which returns
both the function value and the first derivative of the function.
INTEGER j
REAL df,dx,dxold,f,fh,fl,temp,xh,xl使用 rtsafe 與上面 rtnewt 是一模一樣的,請自行練習。
多維度的 Newton-Raphson 方法
多維度的泰勒展開
(以下畫面取自課本)
注意(9.6.6)是矩陣方程式,需要透過先前學過的解線性代數方程式的方法來獲得 dx 。
副程式的使用
SUBROUTINE mnewt(ntrial,x,n,tolx,tolf)
INTEGER n,ntrial,NP
REAL tolf,tolx,x(n)
PARAMETER (NP=15) Up to NP variables.
C USES lubksb,ludcmp,usrfun
Given an initial guess x for a root in n dimensions, take ntrial Newton-Raphson steps to
improve the root. Stop if the root converges in either summed absolute variable increments
tolx or summed absolute function values tolf.
INTEGER i,k,indx(NP)
REAL d,errf,errx,fjac(NP,NP),fvec(NP),p(NP)如同前面有說到,這裏會用到解線性代數方程問題。因此會用到 lubksb 及 ludcmp ,但這是 mnewt 要叫用的,你寫的主程式不會出現叫用它們的動作,記得在編譯連結時要提到這兩個副程式便是。
重要的是,為了讓 mnewt 叫用,使用者必須自行寫一個 usrfun 的副程式,它包含了能給出 F 向量及 J 矩陣的功能。你自己要動手求得函數的微分後公式。
以上是 usrfun 在 mnewt 中被叫用的情行,由其被呼叫的形式可見,(1) usrfun 應宣告為副程式,(2) 依照 x, n, NP, fvec, fjac 的順序定副程式引數的順序(引數名稱通常會與呼叫它的上層程式用的不同),(3) 按這些引數在上層呼叫程式中所被宣告的數值型態,副程式中也作一樣的宣告。
範例主程式(含 usrfun 副程式)如下:
program mnewt_main
implicit nonec integer n_max to define maximum n
integer n_max, i, i_again
parameter (n_max = 16)c integer for mnewt, n has to be smaller than NP=16
integer ntrial,n
parameter (n=2)
real x(n),tolx,tolfwrite(*,*) 'How many repeating steps for Newton methods ?'
read(*,*) ntrial
c write(*,*) 'How many variables is there in your problem ?'
c read(*,*) n
write(*,*) 'Please type in x tol and f tol for mnewt :'
read(*,*) tolx, tolf100 write(*,*) 'What is your inital guess on x(i) vector ?'
read(*,*) (x(i),i=1,n)
call mnewt(ntrial,x,n,tolx,tolf)
write(*,*) 'The root vector is :'
do i=1,n
write(*,*) x(i)
end do101 write(*,*) 'Find root again ? (1=Yes;0=No)'
read(*,*) i_again
if (i_again.eq.1) goto 100
if (i_again.eq.0) stop
goto 101end
subroutine usrfun (x,n,NP,fvec,fjac)
integer n,NP
real x(n),fvec(NP),fjac(NP,NP)fvec(1) = x(2) - x(1)
fvec(2) = x(2) + x(1)
fjac(1,1) = -1
fjac(2,1) = 1
fjac(1,2) = 1
fjac(2,2) = 1end
註:以上的範例是求 F(x,y) 的根,其中 F1(x,y) = y - x、F2(x,y) = y + x。
若 Jacobian 不容易動手推導得到,也可改用數值微分的 fdjac 如下:
如何在你自己寫的 usrfun 中再叫用 fdjac,請看清楚其使用方法說明後用心想一想並確實練習。
牛頓法與碎形 (fractal)
前面曾經警告過大家牛頓法有時也會碰到找不到根的情況,這當然與函數形狀的特殊性有關,而這裏有個有趣的實作大家可以試試看,它會產生碎形 (http://en.wikipedia.org/wiki/Fractal) 的圖形,我們來看以下複變函數的根
依照牛頓法,某個根的猜測位置到下個根的猜測位置間的距離,是在該點取負的函數值再除以在那一點處的斜率。按上面函數的定義,把 Dz 加到 zj 上來得到 zj+1 ,可寫下以下可用來一步步迭代的關係式
在複數平面上的每一個點,都可拿來作為猜測的起始值,看它是否會一步步逼近到滿足原函數的根,若是,則該起始值標白色,若不是則標黑色。如果我們把複數平面上所有的點都標定顏色,則我們會看到碎形,這種圖不管如何放大,都會有重覆類似的結構不斷出現。大家可以寫一個程式,用 pgplot 畫出來看看。
更進一步的細節,可參見我另外編寫的 碎形 單元。
網路上關於碎形圖庫或程式的網站很多,有些甚至融入了藝術化的處理。
http://sprott.physics.wisc.edu/carlson/
http://www.fractalus.com/gumbycat/
混沌藝廊
http://www-chaos.umd.edu/gallery.htmlICM 2006 Benoit Mandelbrot 碎形藝術競賽
http://www.fractalartcontests.com/2006/另外,一本很好的書是 "The Beauty of Fractals",由 H.-O. Petigen 與 P.H. Richter 所著,Springer-Verlag 出版。