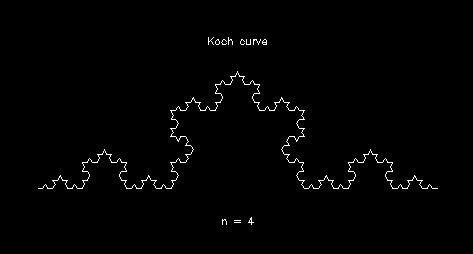碎形

（本單元範例程式全由李明憲老師撰寫，供各位同學參考）

碎形是什麼？

碎形是用來稱一種特殊的幾何圖形，它處處的局部都有著一樣的特徵結構或圖案。由於電腦的輔助。

碎形常見於不斷重覆迭代一個收縮性的函數的極限點集，叫做吸子 (attractor)，一個簡單（但不是碎形）的例子是 f(x) = x²，若從 x = [0,1) 出發，把 x_n+1 = x_n² 一直代下去的話，最後的值會趨近於 0，x=0 這個點就是 f(x) = x² 這個反覆迭代映射的吸子，又如另一個例子是 f(x) = x/2，它最後當然是跑到 x = 0 上。若是 f(x) = -x，則是一直在兩個點之間跳動，它們的吸子都非常簡單。

有些反覆迭代映射的吸子就複雜得多，不是一兩個固定點而己，叫奇異吸子 (strange attractor)，而它既是滿足持定函數不斷映射的結果，當然就有其一定的規律性，尤其是收縮性的映射，就是把點投射到比原來更小的靶範圍內，然而這個吸子上的所有點依定義不會再受映射對應到新的點，可以想像它就會保有局部結構下都仍一再具有此規律性。從這裏大家可以體會為什麼經過不斷的放大去看更精細的構造時，其特徵的圖樣總會不斷出現，就是要這樣才能滿足吸子的定義。

另外，由於碎形所具有的這種特殊性質，也引發了一種定義維度的新觀點。維度可以看作是一個東西其長度的大小與重量的關係。如果其重量隨長度的平方變化，則這個件物是二維的：若是隨長度的立方變化，則是三維的。而以碎形的樣式出現的物件，其重量與長度變化的比例並不是整數，叫做是碎形維度。

大家可以透過自己動手寫程式，來畫出有趣又好玩的碎形。

碎形程式寫作要點

(1) 運算迭代

複數的使用

宣告的方法為 complex a 或 complex z(10,10) 。

複數的常數在 Fortran 裏是寫成 (1.23, 4.56) 這種樣子

如果需要取出其實部或虛部，可用 real(c_num) 或 imag(c_num) 這兩個內建函數；反之，若要將一個實數填入複數中，則可用 c_num = (1.0,0.0)*r_num 這種方法。

演算法

按各種碎形其既定的規則迭代而己，並非求解數學問題。

收斂度判斷

基於迴圈次數

在判定為不收斂之後，記錄已執行的迴圈次數。

基於精確度

使用內建的對數函數 log( ) 來獲得次方

exit 指令

當判斷成立，並且作了適當的處理之後，我們會有需要跳出未跑完的迴圈（放棄剩下的循環不必做），這時候，可以使用 exit 指令來跳出一層的迴圈。它的語法極簡單，只有 exit 而己。

亂數

IFS 類型的碎形會需要用到亂數產生器，普遍而言一個亂數產生器每次被呼叫就會給出一個 0 到 1 之間的不同實數，其出現的機率是相當平均的。我們這裏使用 Numerical Recipes 書中建議提供的 ran2，它均勻度的品質是最好的。另有一個 ran3，其速度比 ran2 快很多。（如果你使用的是 Fortran90 或更新的版本，就有內建的亂數函式可用。）

遞迴式的 (recursive) 副程式呼叫

有一些碎形，像是 Koch 雪花這種被叫做是 regular fractal 者，如果能用遞迴式的副程式呼叫，就能把程式寫得非常簡捷。使用者要找新版本的 Fortran 編譯器，就會支援了（實習環境中的 gfortran 是有支援的，事實上它是 fortran 95）。

(2) 圖形

paper and graph setting

紙張（圖面）大小

圖框、座標與標簽文字

point symbol type

a. coloring

cyclic index

user defined shading

b. magnification

repeating

(3) Repeating

A simple "GOTO" application

rease graph without asking

Mandelbrot 集合

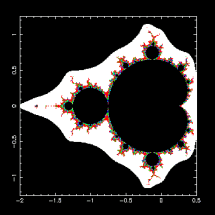
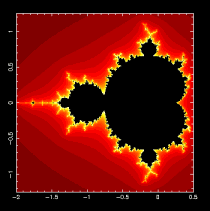
最具代表性也是很多人公最認美麗的碎形，是數學家 Mandelbrot 及其他人的努力研究才引起大家的重視。它是複數平面上的點集合，叫 Mandelbrot Set，M，其定義是所有複數平面上會使反覆迭代映射 z_n+1 = z_n² + c 不會造成 | z_n | 發散的那些 c 值。( z 的初始值要用 (0,0) )

實作示範：一步一步動手寫程式（簡單範例版，不含放大及重覆）

演算法及判定（下面範例程式中的紅色部分）

設定初始 z 值（一律為零）、設定新的 c 值（每次都不同）、反覆迭代映射（每次都檢查是否發散，若是則 c 點標成白色，並且跳出迭代迴圈）

繪圖（下面範例程式中的藍色部分）

pgopen 與 pgclos：開啟及關閉繪圖裝置

papap 與 pgenv：控制圖面的大小以及邊框範圍

pgpt：畫點

pgbbuf 與 pgebuf：開啟及關閉繪圖緩衝區

以下為範例程式： mandel_simple.f mandel_simple.x

program mandelbrot_simple
implicit none
complex c,z_ini,z
integer pgopen,i,j,k,isymbol,n_gen
real c_x_min,c_x_max,c_y_min,c_y_max,c_x,c_y,abs_z

isymbol = -1

write (*,*) 'The program plot Mandelbrot set in a simple way.'
write (*,*)
z_ini = (0.0,0.0)

if ( pgopen('/xwin') .le. 0 ) stop
call pgpap(5.0,1.0)

write (*,*) 'What is the numer of iteration for the mapping ?'
read (*,*) n_gen

c_x_min = -2.0
c_x_max = 0.5
c_y_min = -1.25
c_y_max = 1.25

call pgenv(c_x_min, c_x_max, c_y_min, c_y_max, 1, 0)

do j=1,500
　c_x = c_x_min + j*(c_x_max-c_x_min)/500
　call pgbbuf
　do k=1,500
　　c_y = c_y_min + k*(c_y_max-c_y_min)/500
　　c = (1.0,0.0)*c_x + (0.0,1.0)*c_y
　　z = z_ini
　　do i=1,n_gen
　　　z = z*z + c
　　　abs_z = conjg(z)*z
　　　if (abs_z.gt.10e+10) then
　　　　call pgpt(1,c_x,c_y,isymbol)
　　　　exit
　　　endif
　　end do
　end do
　call pgebuf
end do

call pgclos
end

以下是完整的程式，具有放大及詢問使用者多次重畫的功能，請大家比較參考：

mandelbrot.f mandelbrot.x mandelbrot.f.txt

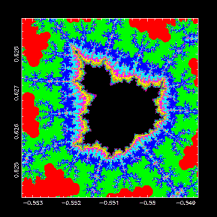
加入了漸層色彩指標設定的進階功能：

mandel_shade.f mandel_shade.x mandel_shade.f.txt

維基百科上的精采資料
http://en.wikipedia.org/wiki/Mandelbrot_set

Julia Set

Julia Set 產生的方法和 Mandelblort Set 一樣是檢驗迭代 f(z) = z*z + c 的發散性，但是是掃遍不同的 z 而不是 c。下圖左右分別是 c = (0.2,0.6) 及 c = (0.0,1.0) 的結果：

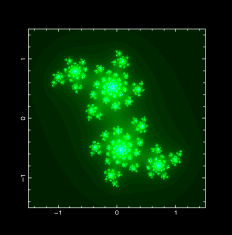
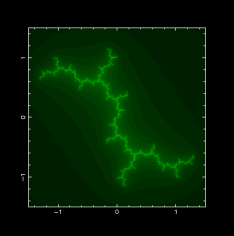
julia_shade.f julia_shade.f.txt

牛頓法

牛頓法是一種利用斜率方向的引導來求函數根的方法，這種方法在猜測點離根夠近（具體地說是在根之處的斜率與猜測點處的斜率間的變化是單調性的）時是很有效率的，然而對於不同的猜測點，從那裏出發依斜率方向去找根所會需要用到的迭代步數會比別的起始點多，在有些函數甚至會越追離根越遠。牛頓法由於具有固定的演算公式，因此若是初始猜測位置固定，處理的函數也一樣的話，

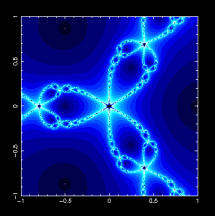
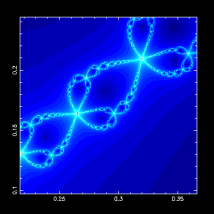
以牛頓法求複數函數 f(z) = z³ - 1 的根，就是相當於是進行

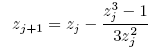
的反覆迭代問題

z³ - 1 = 0 要求滿足這個方程式的解，一定是具有 2π/3 對稱性的。

newton.f newton.x newton.f.txt

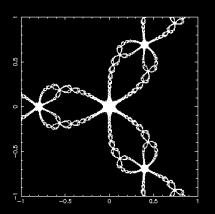
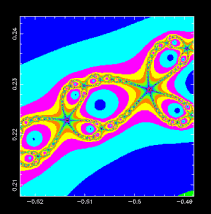
newton_shade.f newton_shade.x newton_shade.f.txt

Koch 曲線

koch.f koch.f.txt koch.x

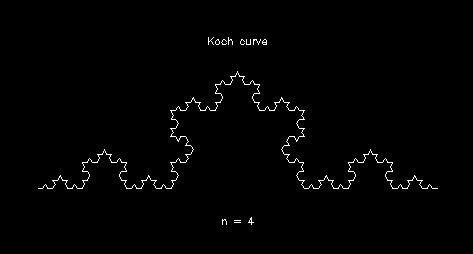
koch_snow.f koch_snow.f.txt koch_snow.x

請自己做做看以下的圖形（可利用 PGPLOT 畫多邊形與填色的功能）

蕨葉 (Fern Leaf)

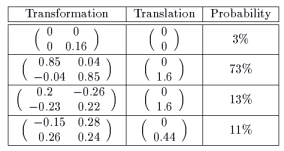
另一種產生碎形的方法是所謂的 IFS (Iterated Function Systems) ，它的吸子所構成的點集，可讓我們設計成類似蕨葉的形態，其演算法如下：

x_n+1 = ax_n + by_n + e

y_n+1 = cx_n + dy_n + f

a b c d e f p

0.00 0.00 0.00 0.16 0.00 0.00 0.01

0.85 0.04 -0.04 0.85 0.00 1.60 0.85

0.20 -0.26 0.23 0.22 0.00 1.60 0.07

-0.15 0.28 0.26 0.24 0.00 0.44 0.07

上表共有四組，最後一列的 p 是代表要使用該組演算式的機率。也可以表示成下式：

畫出來的結果是這個樣子：

fern.f fern.x fern.f.txt ran2.f

另一種，很像是路邊不知名雜草長出來的穗的部分：

weed.f weed.x weed.f.txt ran2.f

另有楓葉的 IFS（請自己做做看）

a b c d e f p

0.14 0.01 0.00 0.51 -0.08 -1.31 0.10

0.43 0.52 -0.45 0.50 1.49 -0.75 0.35

0.45 -0.49 0.47 0.47 -1.62 -0.74 0.35

0.49 0.00 0.00 0.51 0.02 1.62 0.20

maple.f ran2.f

為什麼會有如圖中這般的自我類似？因為這些點都是滿足迭代函數系統的吸子，也就是說，這些點都滿足 "代了很多次也不會跑掉的特性"。能夠在這樣的條件被篩選出來的點，呈現在畫面上，形成了賞心悅目的效果。

以蕨葉點集為例，它是由四個收縮性的映射所構成，當一個起始點被某個映射函數處理之後，就落入較小的特定範圍之中，但再緊接下來，它有可能被另一個映射函數處理，於是落入在原範圍之下的更小的另一種點分佈排列模式的範圍。你可以想像如此繼續迭代下去（過程中不同的四個函數都有用到 <問，那機率是做什麼用的？>），則每一個微小局部一定都具有類似的圖形，也就是同時具有滿足四種函數之吸子的構造。

機率可以不同

來源：http://zeuscat.com/andrew/chaos/spleenwort.fern.html

The Collage Theorem
http://www.cut-the-knot.org/ctk/ifs.shtml

Fern Functions
http://mathworld.wolfram.com/BarnsleysFern.html

葉子的形狀
http://www.fukuoka-edu.ac.jp/~fukuhara/jikken/leaf_shape.html

葉脈網絡
http://www.nibb.ac.jp/math/work_fujita.html

碎形與自然

由於碎形所具有的自我類似的特性，使它與許多自然界中存在的幾何圖形有些相像之處。例如枝葉的分叉、河流與葉脈的分支、山嶽的輪廓、雲的形狀、濺起的海浪、紊流與亂流，等等。可謂一沙一世界、一花一天堂。（感謝網路上之照片來源）

碎形的應用

影像處理

http://fractalfoundation.org/OFC/OFC-12-1.html

http://fractalfoundation.org/OFC/OFC-12-2.html

http://fractalfoundation.org/OFC/OFC-12-3.html

碎形藝術

網路上可見許多結合碎形與藝術的作品。

http://sprott.physics.wisc.edu/carlson/

http://www.fractalus.com/gumbycat/

混沌藝廊
http://www-chaos.umd.edu/gallery.html

ICM 2006 Benoit Mandelbrot 碎形藝術競賽
http://www.fractalartcontests.com/2006/

殘形美學與國畫
http://members.tripod.com/gia_5/fractal/aesth.htm

其他注意事項

本節範例程式皆使用單精度，若要達到較佳的放大級數，則應用雙精度。

參考書籍

一本很好的書是 "The Beauty of Fractals"，由 H.-O. Petigen 與 P.H. Richter 所著，Springer-Verlag 出版。

網路資源

Fractal Mathematics
http://www.hiddendimension.com/Mathematics_Main.html

Cynthia Lanius' Lessons: A Fractals Lesson - Introduction
http://math.rice.edu/~lanius/fractals/

Fractals
http://www.ocf.berkeley.edu/~wwu/fractals/fractals.html

很棒的動畫
http://www.stanford.edu/~willywu/downloads/xaos1.mpg

用 XaoS 軟體做的
http://wmi.math.u-szeged.hu/xaos/doku.php?id=main

Fractal Art
http://www.fractalus.com/info/manifesto.htm

http://math.rice.edu/~lanius/frac/

Fractals in Nature and How to Measure Them
http://www.fbmn.fh-darmstadt.de/home/sandau/biofractals/abstract_sfi.html

Julia and Mandelbrot Sets (Clark University)
http://aleph0.clarku.edu/~djoyce/julia/index.html

維基百科：Julia Set
http://en.wikipedia.org/wiki/Julia_set

維基百科：De Rham curve
http://en.wikipedia.org/wiki/De_Rham_curve

維基百科：Iterated Function System (IFS)
http://en.wikipedia.org/wiki/Iterated_function_system

利用培基 (BASIC) 語言寫碎形的網頁（外部資源）

初學者容易入門的 BASIC 語言：Decimal BASIC 官網、下載、英文網址、手冊、快速入門

BASIC 與自我類似 (Self-similarity)
http://www.geocities.jp/thinking_math_education/self-sim/self-sim.htm

BASIC 與碎形
http://www.geocities.jp/thinking_math_education/fractal/fractals.htm

True BASIC
http://www.truebasic.com/

Free BASIC Compilers and Interpreters
http://www.thefreecountry.com/compilers/basic.shtml

a	b	c	d	e	f	p
0.00	0.00	0.00	0.16	0.00	0.00	0.01
0.85	0.04	-0.04	0.85	0.00	1.60	0.85
0.20	-0.26	0.23	0.22	0.00	1.60	0.07
-0.15	0.28	0.26	0.24	0.00	0.44	0.07

a	b	c	d	e	f	p
0.14	0.01	0.00	0.51	-0.08	-1.31	0.10
0.43	0.52	-0.45	0.50	1.49	-0.75	0.35
0.45	-0.49	0.47	0.47	-1.62	-0.74	0.35
0.49	0.00	0.00	0.51	0.02	1.62	0.20