本單元所會用到的副程式,不含使用者所需要寫的,一共有十個之多,請大家注意。(所有 newt 相關與 odeint 相關的都要用到,裏頭包含:全域收斂牛頓法需用 newt、lnsrch、fmin、fdjac、ludcmp、lubksb ;步幅調控隆巨庫塔法需用 odeint、 rkqs、rkck;射擊法需用 shoot。)
本節的主要副程式是 shoot ,它會傳入初始猜測值,並驅動 rkqs (有調適步幅的 Runge-Kutta 解常微方方法)走完一條解。很重要的是它必須被(全域收斂的)牛頓法 newt 叫用(我們前面有介紹過,newt 的用法相當單純),因此請注意到這裏 shoot.f 檔內實際的副程式名是 funcv 。

(副程式)
使用者必須自行提供的副程式在這裏則有三個,分別是 (1) load、(2) score、(3) derivs。再次提醒,shoot.f 副程式是叫作 funcv,這次的 funcv 不必使用者自己寫。
(公共區塊)
撰寫主程式時,要注意 common block 的設定,由 shoot 的內容可以知道,有些變數是要透過 common blcok 傳給副程式的,另外,如果要畫出曲線,則 rkqs 的中間過程結果也要由 common blcok 取出來。請注意課本附的 shoot (funcv) 副程式會把 kmax 設成 0 ,因此不會作中間過程的儲存,想用到這些中間結果就要自行把 shoot 中之 kmax 改設(最多不能超過 KMAXX,作法參考 odeint 之說明),或是利用使用者自己寫的副程式中存取 common block ,在呼叫 odeint 之前就先把 kmax 再改成非零的值。
(parameter 與 common)
另外,宣告了 parameter 的束西,也不能放在 common 中,比方說,nvar 有被宣告在 common block 中,nvar 就不能被定為 parameter,有需要作 nvar 大小陣到宣告的地方,就要另行用其他參數或直接給數字來宣告。 值得一提的是,odeint 內部雖有宣告用到 ystart(nvar) 這樣的東西,但 ystart 是由外部 y 傳進去給 odeint 的,且 nvar 也自外部傳入,按 Fortran 向副程式傳遞陣列的方式,是只傳陣列的起始位置,因此在 odeint 副程式中並沒有新開記憶體貯存的空間,我們因此不必把 nvar 在上層程式設定成常數,畢竟不會真的在 odeint 中有配置 nvar 大小之陣列這種動作,事實上,此系列副程式套組己預設 nvar 的上限為 NMAX,也就是 50,已絕對夠用了。
(積分初始值)
使用者所要寫的主程式,它會呼叫 newt, 主程式要先讀入初始猜測的 V(n2),傳給 newt 當作是要求的根,然後 newt 傳給 shoot (funcv),再由 funcv 去呼叫 odeint,odeint 當然會需要 vstart(nvar) 來作開始,我們注意在函式 shoot (也就是這裏 newt 下的 funcv)有先呼叫一個 load(x1,v,y) ,而 funcv 只有 V(n2) 傳進來,因此 ystart(nvar) 是要在先利用 load 來組合出,課文中程式說明也是這樣講的:
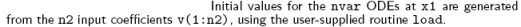
x1 與 x2 在整個運算流程中一直是求解範圍的起始點與最終點沒有改變,common block /caller/ 有它定義。請小心 common block 中有的東西就不允許再寫成傳引數的動作了,也就是說 load 與 score 都不能寫成要使用 /caller/ 公共區塊,因為從 shoot 可看見它們以傳入引數的方式處理 x1 與 x2,當然事實上也就沒有這個必要 common block。
例如,求解一個二階常微分方程式,而邊界條件是 y(x1) = 0.0、y(x2) = 0.0 時,則其 load 副程式範例如下:
subroutine load(x1,v,y)
real x1,v,y(2)
y(1) = 0.0
y(2) = v
end
註:為什麼這裏要傳 x1 進去?這是因為邊界條件的計算視題目的要求也可能會用到 x 值。雖然在本例中沒有用到,但為了完整性其副程式的引數仍要設計成有傳入。
雖然 n2 在 shoot (funcv) 中有定義,但卻沒有以引數方式傳入 score 副程式,你可以考慮直接把陣列大小定下去或是間接另行找一個新變數來使用,如以下範例(一樣邊界條件是 y(x1) = 0.0、y(x2) = 0.0):
subroutine score(x2,y,f)
integer n2
parameter (n2=1)
real x2,y(2),f(n2)
f(1) = y(1) - 0.0
write(*,*) 'f value in subroutine score is :', f(1)
end
提醒大家,把邊界條件達成與否的指標函數 f 的值印出來是很有用的,另外,在呼叫完 newt(也就是找完了根之後),把最終符合邊界條件的 V 值印出也很可以知道與猜測值差多少。
再多給一組例子,假設邊界條件為 y'(x1) = 1.0、y'(x2) = 2.5,則 load 與 score 的寫法分別為:
subroutine load(x1,v,y)
real x1,v,y(2)
y(1) = v
y(2) = 1.0
end
subroutine score(x2,y,f)
integer n2
parameter (n2=1)
real x2,y(2),f(n2)
f(1) = y(2) - 2.5
write(*,*) 'f value in subroutine score is :', f(1)
end
(修改副程式中的設定)
雖然課本副程式基本上都是不需要修改就可以使用的,但本節的程式組合了兩大數值方法,其中有很多調整性參數在程式碼中都是先給了預測值,像如果要保留中間過程的話,前面的提到的 kmax 就要打開(也就是說,在 shoot.f 中把原本的 kmax = 0 改成為 kmax = KMAXX )。另外,控制 odeint 精密度的 EPS 也可視你自已的需要而調整,它會直接影響中間過程的點數。至於 dxsav 是調整多大的 rkqs 步幅值就要儲存的參數,想存多個點就設小一點。
(邏輯變數 check)
如果邏輯變數 check 的結果為真 (T) ,代表計算有些不順利需要檢查;如果是假 (F),則它表計算有正常結束而不需要檢查。
(對初始值的敏感度)
在實做的過程中,你會發現對不同的問題對初始值的敏感度是不一樣的。有些比較困難的情況,不適當的猜測初始值會導致 ludcmp 無法求解,通常多試幾個初始猜測值可次解決問題。
(與 PGPLOT 的搭配)
若要與 PGPLOT 繪圖副程式庫的搭配,則在編譯時還要再鏈結 pgplot 與 X11 兩個函式庫,例如:
gfortran -o my_exe.x my_prog.f -lX11 -L /usr/local/pgplot -lpgplot
一個實際可用的範例主程式 shoot_main_pgsub.f,在此列出以供參考:
program shoot_main_pgsub
implicit none
integer i,n2,nvar,kmax,kount,KMAXX,NMAX
parameter (n2=1,NMAX=50,KMAXX=200)
real f(n2),V(n2),x1,x2,dxsav,xp(KMAXX),yp(NMAX,KMAXX)
logical check
common /caller/ x1,x2,nvar
common /path/ kmax,kount,dxsav,xp,yp
nvar = 2
kmax = KMAXX
dxsav = 0.01
write(*,*) 'Please type in beginning and final x : x1 and x2'
read (*,*) x1, x2
write(*,*) 'What is the guess (vector) of the initial condition ?'
read (*,*) (V(i),i=1,n2)
call newt(V,n2,check)
write(*,*) 'n2 is ;', n2
write(*,*) 'The final value of V is :', V
write(*,*) 'check of newt is', check
write(*,*) 'koumt is', kount
call pg_draw_path()
end
subroutine load(x1,V,y)
real x1,V,y(2)
y(1) = 0.0
y(2) = V
end
subroutine score(x2,y,f)
integer n2
parameter (n2=1)
real x2,y(2),f(n2)
f(1) = y(1) - 0.0
write(*,*) 'f value in subroutine score is :', f(1)
end
subroutine derivs(x,y,dydx)
real x,y(2),dydx(2)
dydx(1) = y(2)
dydx(2) = -y(1)
end
subroutine pg_draw_path()
implicit none
integer pgopen,i,j,nvar,nvar1,kmax,kount,KMAXX,NMAX
parameter (nvar1=2,NMAX=50,KMAXX=200)
real x1,x2,dxsav,xp(KMAXX),yp(NMAX,KMAXX)
c For pgplot
real y_min(nvar1),y_max(nvar1),yy(KMAXX),y_extra
common /caller/ x1,x2,nvar
common /path/ kmax,kount,dxsav,xp,yp
c Find Max and min values of yi(x), but here we will use only y1(x).
do i=1,nvar
y_max(i)= yp(i,1)
y_min(i)= yp(i,1)
end do
do i=1,nvar
do j=2,kount
if (yp(i,j).gt.y_max(i)) y_max(i)=yp(i,j)
if (yp(i,j).lt.y_min(i)) y_min(i)=yp(i,j)
end do
end do
c Copy y(1,1:nstep) to yy(1:nstep) for PGLINE plotting
do i=1,kount
yy(i) = yp(1,i)
end do
c Intermidiate reult check
c do i=1,kount
c write(*,200) i,xp(i),i, yy(i)
c 200 format(1x,'x(',i3,') is ',f5.2,' y(',i3,') is ',f5.2)
c end do
c Start plotting
y_extra = 0.1*(y_max(1)-y_min(1))
if (pgopen('/xwin').le.0) stop
call pgpap(6.0,0.75)
call pgenv (x1,x2,y_min(1)-y_extra,y_max(1)+y_extra,0,0)
call pgline(kount,xp,yy)
call pgsci(2)
call pgpt(kount,xp,yy,9)
call pgclos
end
![]()
![]()
