分析的步驟:畫圖、寫下方程式、找通解
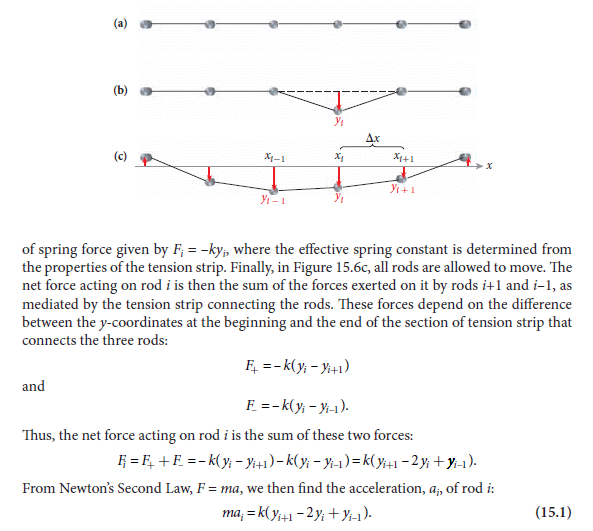
上式右手邊相當於是是二次微分,至於要除之的 (Δx)2 將會來自 Δk = k/Δx 及 Δm = μ Δx 各一個。如此,式子中各有對時間及對空間微分兩次,這即是波動方程式的特徵。
以上的推導不管是縱波或是橫波都適用,原因:彈性學已學過剪應力與剪應變,因此有一樣的線性公式可以使用。
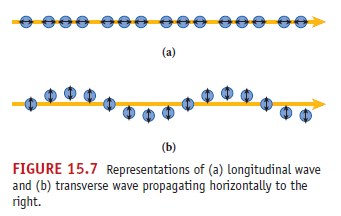
另一種推導(Halliday 課本)
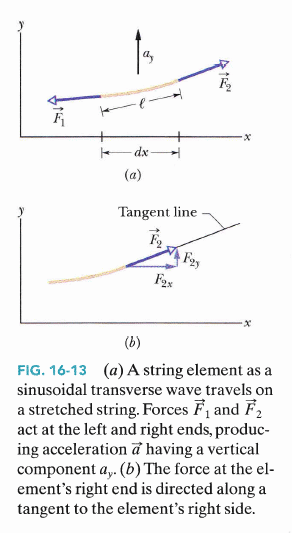
見推導 連結
波動
波是自然界的重要本質之一 ,它具有規律的持質,了以及傳播能量的能力。在微觀的世界裏,它甚至是主宰物質行為的準則。
波會在空間中傳播動盪但一般而言不傳送物質 (像擾動平靜的水池以及運動場觀眾席上的人浪)。有些波需要透過媒介 (介質) ,另外一些如電磁波就不需要。本章僅探討有媒介質的波。
耦合振子
分析的步驟:畫圖、寫下方程式、找通解
上式右手邊相當於是是二次微分,至於要除之的 (Δx)2 將會來自 Δk = k/Δx 及 Δm = μ Δx 各一個。如此,式子中各有對時間及對空間微分兩次,這即是波動方程式的特徵。
以上的推導不管是縱波或是橫波都適用,原因:彈性學已學過剪應力與剪應變,因此有一樣的線性公式可以使用。
另一種推導(Halliday 課本)
見推導 連結
波的數學描述
波的最重要特徵就是空間的重覆性與時間的重覆性。因此本節的兩個基本量是周期與波長。
最常用高重要的是正弦波 (sinusolidal waves)
解釋名詞
波前:振幅最大值處
周期 T :讓三角函數走完一個函數值變化(之後重覆)所需要的時間,見上圖
A sin ( ω(t=0) + φ0 ) = A sin ( 2π + φ0 )
2π= ωT
角頻率 ω:ω= 2π/ T
頻率 f :f = 1 / T
波長 λ:相鄰兩個最大值間的距離,見上圖
波速 v :v = λν
由前已知走一個波長的時間是一周期,故波速為波長除以周期,即長乘以頻率
波形、波數、相位
前面利用振盪的圖像各自建立了時間與空間重覆性的情形,即當時暫先想像振子位於 x=0 處。要想以數學函數形式把完整而可在空間中傳播的波表示出來,考慮波前要花 t = x / v 的時間來移動 x 那麼多的距離。只須要把 t 改寫為 t - x / v ,一樣放到原本時間函數 t 所在的地方。
y(t) = A sin ( ω ( t - x / v ) + θ0 )
前已有 ω = 2πf
y(t) = A sin ( 2πf ( t - x / v ) + θ0)
y(t) = A sin ( 2πf t - 2πfx / v + θ0)
y(t) = A sin ( 2πf t - 2πf x /(λf) + θ0)
y(t) = A sin ( 2πf t - 2πx /λ + θ0)
y(t) = A sin ( (2π/T) t - (2π/λ) x + θ0)
其中 2π/T = ω
我們比照來定 2π/λ= κ
則得
y(t) = A sin (ω t - κx + θ0)
如果我們一間始是全部定在某一個時刻,而問過了一段時間之後波前移到那裏,則會有
y(t) = A sin ( κx - ωt + φ0 )
這與上式是等效的結果,因拿為 sin(-x) = - sin(x) = sin(π + x)
φ0 = π - φ0
後者的形式比較常用,以下用之。
註:在前面我們已經定出了角頻率與周期的關係,其意義是單位時間長度裏會有幾個波,如下
ω= 2π/ T
在三角函數波 A sin ( κx - ωt + φ0 ) 的定義域 κx - ωt + φ0 用與角頻率(時間)相同的方式來看待空間的係數,我們就有波數(又叫做波向量),
κ = 2π/ λ
其意義是單位空間長度間裏會有幾個波。
總之,波的數學描述可以是
y(t) = A sin ( κx - ωt + φ0 )
其中,波的相位 φ = κx - ωt + φ0
"波前" 位於某固定 "相位" 角度
φ = C = κx - ωt + φ0
即
x = (ω/κ) t + (φ0+ C ) /κ
故
dx/dt = ω/κ
這叫做 "相" 速度,也就是 "波前" 的速度,即下面重要的關係式:
v = ω/ κ
波動方程式的推導
波動方程式的特徵,是對時間微分兩次也對空間微分兩次,如下:
∂2 y(x,t) /∂t2 - v2 ∂2 y(x,t) /∂x2 = 0
過程請見推導 15.1
"波速"自然出現於波動方程式中
波動方程式中,波速自然出現,故它是比較基本的量。一個介質有一定的波速(如空氣、水及鋼),而不同搭配的頻率與波長都有可能,只要保持乘積是波長即可。
這與一個單一振子,只有一個自然頻率,並不相同。事實上,兩個自由度的耦合振子對,有兩個自然頻率,n 個自由度的耦合振子群,共有 n 個自然頻率。一個連續介質可視為有無數個振子耦合在一起,因此頻率有無限多種(另外,以晶體為例,波長有最小值,因此頻率有最大值)。
波動方程式的解
以正弦波 y(t) = A sin ( κx - ωt + φ0 ) 代入驗證,微分 sin 得 cos,再微分 cos 得 -sin ,可看出確定確為其解,只要其中的參數滿足
ω2 - v2 κ2 = 0
而前面已經由波前的移動推得 v = ω/ κ,因此上式自動成立,故正弦波確實是波動方程式的解。
廣義的解形式
一個值得注意的事情是,正弦波已經是最一般性的情況了嗎?不是的,任何可微分函數其定義域具有 κx - ωt 的形式,都是波動方程式的解。另外,習慣上 κ和 ω我們都只用正值,因此 Y(κx - ωt ) 與 Y( κx + ωt ) ,前者代表向正 x 方向傳播、後者代表向負 x 方向傳播,都是一般解。
從微分的鏈鎖率 可以看出,
df(g) / dx = (df/dg) (dg/dx)
df(g) / dt = (df/dg) (dg/dt)
我們不管是在做對時間座標微分的部分亦或是做對空間座標微分的部分,
g(x,t) = κx - ωt 一定會導致 ω2 - v2 κ2 = 0 的滿足
奇怪?那我們前面還做那麼多正弦波分析,怎麼回事?莊孝維嗎?
(上述論寫點在二維及三維也對?振幅會衰減怎辦?邊界條件如何滿足?)
弦上的波
弦樂器因其上之弦振動而發聲,
弦,顧名思義,兩頭是固定住的
如果我們把弦的振盪看作是耦合在一起的振子,回復力與伸長量成正比,即繩張力(注意不是周期 T)T = k Δx ,其中 k = √() 則我們知道其波速是
k Δx2 = m v2
故
v = √(k/m) Δx =
二維及三維的波
由於能量守恆但分散開來, 因此振幅隨距離而變小(問 : 這是另外要求的,還是包含在波動方程式之中必然的結果?)
(以下見課本)
球面波
平面波
表面波
地震波
範例 15.2 測量地球的熔融核心大小
波的能量、功率與強度(見課本)
能量
功率
強度
疊加原理與干涉
以 y(x,t) = A exp {- (x - vt)2 } 為例,它叫做 高斯函數 ,其定義域也具有 x - v t 的形式,因此也是波動方程式的解。
範例 15.3 波脈衝的疊加
由於疊加原理,干涉現象就會發生。
相量 (Phasor)
一種處理(加總)三角函數求解簡便的方法
駐波與共振
兩個振幅相同、行進速度相反的正弦波,其疊加的和
利用三角形和差化積公式
sin α ± sin β = sin α cos β± cos αsin β
可得
y(t) = A sin ( κx - ωt ) + A sin ( κx + ωt ) = 2A sin (κx ) cos (ωt )
即駐波。
弦上的駐波
產生駐波是樂器發出樂音的基本原因。前面有提到,弦張力與質量決定頻率,對於駐波而言,又多了一個弦長的
λn = 2L / n , n ∈N
v = √(T/μ)
故
fn = v / λn = n √[ T / ( 4 L2μ) ]
因此結論是,弦越短越高音、弦越輕越高音、弦越緊越高音,另外,演奏時如果把手按住弦的正中間,還可產生次諧頻音(下一個八度音)。
二維駐波的圖樣可在白砂黑振動板的實驗中看到,
經典問題:我們可以聽出鼓的形狀嗎?
波的研究
微波工程模擬
弦論(駐波)
物質波
重力波
問題:一種介質上是否只有一種波速?
是,從波動方程式的推導結果,我們看到與波速是最基本的,至於它構成的物理量是繩張力、彈性常數與介質密度有關。
水波有折射(及反射)的效應嗎?有,深淺不同會有。繩波的介質疏密不同間也有。波速不同就有折射。
補充;波的群速度
波的色散關係,是由 ω(κ) 函數所決定,至於為何取這兩個值,可理解拿 f 與 lamda 來看也是一樣的
波的群速度定義為 vg ≡∂ω / ∂κ ,不同於相速度的 vp ≡ ω / κ。
真空中所有光速一樣,是沒有色散的。有物質(電介質)時,寫下來的波動方程式之速度平方係數已經不一樣了,因此波速直接就是不同。
問題:如何在弦上(繩上)產生一個脈衝?
如何以數學形式描述一個脈衝?脈衝是是否滿足波動方程式?
許多書籍的圖形示意中,脈衝是全正的振幅(反射波則是全負),要產生這樣全正振幅的的波,外力輸入的快慢或大小,以及本身是否有阻尼這件事,要如何搭配才能符合產生的條件?
問題:How fast does a photo travel ? How fast does a ponon travel ? Is these questions even meaningful ?
問題:Thermo-conductivity of an ideal crystal, is it related to its sound speed ?