右手系
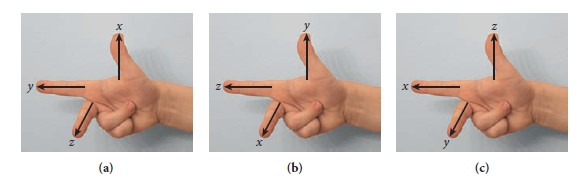
定義
r = (x, y, z) = x ex + y ey + z ez
v = (vx, vy, vz) = vx ex + vy ey + vz ez
v = dr/dt = dx/dt ex + dy/dt ey + dz/dt ez
因此vx= dx/dt ; vy= dy/dt ; vz = dz/dt
其中基底座標 ex、ey、ez 不隨重間改變,因此無導數變化。
向量 與 二、三維的運動
速度、速度分量、向量、向量分量的處理
"分別處理,是否可以?"
向量空間
介紹向量
什麼是向量?
答案(中學版)
有大小、有方向的量
答案(大學版)
滿足向量的座標變換規則的量
基底向量與向量的基底展開
V = Vx ex + Vy ey + Vz ez
常使用正交基底 ei .ej = δ ij
以數學式表示物理向量(常見於物理定律)
例如:f = m a
問題思考:
選定一個座標系,就有一特定的 x 分量及 y 分量。
我們可以各自處理分量的運動虧程式再結各起本嗎?
是什麼保證我們可以就各個分量來處理?
檢驗標準:大小有沒有相等?方向是不是一樣?
座標轉換規則已經保證,我們處理的是同一個向量。
只要把分開處理的分量按向量基底展開
衍生性質:正交座標轉換會保守長度
向量與座標轉換間的關係
座標轉動與基底變換(板書)
正交歸一性
向量空間
函數空間
座標變換下,物理定律的不變性
三維座標系統
右手系
定義
r = (x, y, z) = x ex + y ey + z ez
v = (vx, vy, vz) = vx ex + vy ey + vz ez
v = dr/dt = dx/dt ex + dy/dt ey + dz/dt ez
因此vx= dx/dt ; vy= dy/dt ; vz = dz/dt
其中基底座標 ex、ey、ez 不隨重間改變,因此無導數變化。
速度與加速度
aave = (v1 - v2) / (t2 - t1)
注意分母是純量
理想拋射體運動
r = (x, y) = x ex + y ey
v = (vx, vy) = vx ex + vy ey = ( dx/dt, dy/dt ) = dx/dt ex + dy/dt ey
a = (0, -g) = -g ey
x 方向
x = x0 + vx0 t
vx = vx0
y 方向
y = y 0 + vy0 t - 1/2 g t2
y = y 0 + vy t
vy = vy0 - gt
vy = 1/2 (vy + vy0)
vy2 = vy02 - 2g(y - y0)
有上列(七個)方程式我們可以得出任何時刻軌跡
例 3.1:射猴子
以麻醉槍射從動物園逃走的猴子,但此猴被槍聲嚇到會放手 (don't ask me why)。怎麼瞄?
拋射體軌跡的形狀
整理出 y(x)
拋物線 parabola
最大高度與最大射程
見課本推導及例題
真實拋射體:空氣阻力效應
相對運動
例題、習題、作業 與 討論
2-* 無空氣阻力時,在平地上最遠拋射積來自 45 度仰角(證明詳解見課本)。
助教示範推導:Ch2-8 再論等加速度運動
4-7 砲擊海盜船
5-4(學生自行閱讀)
5-5 光滑斜面加速度
5-6 雲霄飛車
7-2 斜向施力求作功
7-5 斜面拉上之重力作功
7-8 彈力作功
8-3 水滑梯求末速
討論
雨天過街走或跑?(假設身體為矩形,要考慮雨是直打或斜打)
磚磈上下綁繩拉斷那根?
作業
牛頓生平及其科學域就小傳(限手寫)