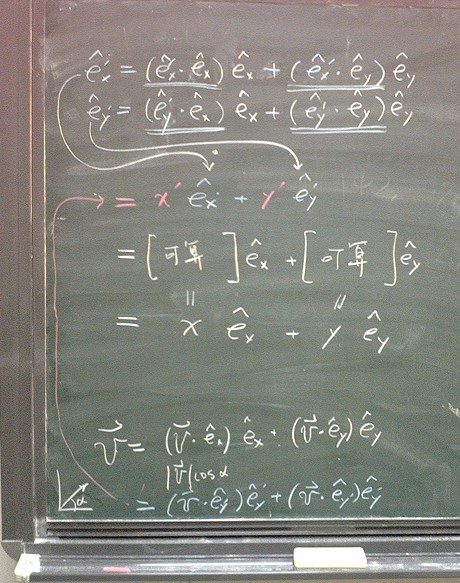
回家作業：己知座標轉動了 α 角，則新座標分量 (x', y') 要怎樣利用舊座標分量 (x, y) 來表示？
幾何 II
向量、座標與基底
幾何學從形狀的學問，透過解析幾何的建立，以座標（向量的分量）來描述空間中的點、線、面、體，賦與了這些物件上函數的意義。
然而，分量所呈現的值，會因為座標軸（基底向量）取法的得不同而有不同。能取到一個比敕好的基底向量來做座標軸，對問題、方程式的簡化是很有幫助的。舉個例子說，橢圓方程式在取了長、短軸作為座標軸之後，形式就變得簡化很多。
（例如，橢圓方程方 4( 3x - 4y + 1)2 + 3 ( 4x + 3y -7 )2 = 900 ）
座標轉動與基底變換
回家作業：己知座標轉動了 α 角，則新座標分量 (x', y') 要怎樣利用舊座標分量 (x, y) 來表示？
由正交(歸一)座標系獲得的啟發：
(vx,vy,vz) dot (ux,uy,uz) = vxux+vyuy+vzuz
f(x') = ∫ f(x)δ(x-x') dx
其中 δ(x) = ∞ , if x = 0= 0, if x ≠ 0
又 ∫{-ε, ε} δ(x) dx = 1, where ε > 0
（不要以為這樣子純想像的抽象函數不一定是存在,它真的可以裝一般行為良好的、具有單一峰值的函數，逐漸逼近而得到。例如適當歸一化了的常態分佈函數，就可以拿來做。）
f_vec=f(x)=(fx1,fx2,fx3,.....)
g_vec=g(x)=(gx1,gx2,gx3,.....)
f_vec dot g_vec= fx1gx1+fx2gx2+fx3gx3+.....
但是現在有一個問題，切割到無限多沒完沒了，數值爆掉不可處理。（就算你堅持可以想像、可以理解，別忘了不能比大小、不能加減乘除、不能算！那就沒什麼用了）
補救一下
重新定義 f_vec dot g_vec = (原來的寫法) / N
另外有一件事情，內積的結果其單位
x 屬於 {a,b}
同乘同除以 b - a ，上式 = (原來的寫法) [(b - a)/(b - a)]/N = [1/(b - a)] (原來的寫法 ) (b - a)/N
最後 (b-a)/N 這個部份 即為 Δx，則
內積 = (b - a)-1 Σ f(x)g(x) Δx
當 N 趨向無限大
內積 = (b - a)-1 ∫ f(x)g(x) dx
我們可以定義符號：: v dot u = < v | u >, 其中 v = | v >, u = | u >
同時 f dot g = < f | g >
沒學積分，在高等數學中連內積(投影)都沒辦法做。
所以，存在函數空間，使得任意 函數 f = Σ{all x'} fx' ex'
其中 ex' =
且 <ex' | ex"> = δx'x" " if x' = x" " , δx'x" = 1; if x'≠ x" ", δx'x"=0
這裏的 ex' 就是 δ(x-x'),
注意，基底也是可以變換的，但(函數)內積的規則仍繼續可用
補充話題：群論（什麼是群？）
能進行二元運算的操作，收集成為一個集合，其中每一個元素
封閉性（for all A, B ∈ G, AB ∈ G）
單位元素 I 存在，使得 對於所有（ A, A I = I A = A
反元素存在（∀A ∈G, ∃A-1 ∋A-1 A = A A-1 = I
為什麼數學家要自嗨定出這樣的東西
範例：旋轉
元素：轉動某角度
封閉性：轉、再轉，等同於轉一次
單位元素存在：零度不轉也是一種轉
反元素存在：反轉
因此，所有的轉動構成一個群
函數空間
基底函數與其正交性、完備性
函數能不能像向量那樣以基底（基底函數）來展開？
向量怎樣定正交？（答案：內積為零）
內積的定義：
http://en.wikipedia.org/wiki/Inner_product_space
兩個函數怎樣定內積？（方法之一：相乘並積分）
函數空間裏的內積
(1) 定義與範例
見內積的一般性定義
(2) 投影與分量
投影本身就是一個非常幾何的名詞
以三角函數作為基底
富利葉 (Fourier) 級數
先看下列的性質：
（以上這些積分如果不會做，也可以寫個程式來計算驗證。）
對於任何週期性函數，都可以用些正弦與餘弦函數展開，如下：
基本技巧 sin(x)sin(y) 怎麼積分
積化和差
如果忘記怎麼證明 : eiθ = cosθ + i sinθ
如果定義域是長度而不是角度
http://mathworld.wolfram.com/FourierSeries.html
從上面的改寫，f(x) 與 An 之間的 1-1 對應更加明顯了。
f(x) 是 -L ~ L 的週期，如果 L → ∞ 則 f(x) 與 An 之間的關係也完全適用
定義 2 nπ/ L = k ，則 L 趨近無限大時，k 變成連續的所以 An = A(k)，索性寫成 F(k)。
（那，原本一個週期之外還有不斷重覆的其他週期，怎辦？仔細想想，我們已經定了 f(x) 從 - ∞ ~ ∞，說它會在 ∞ ~ 2 ∞ 再重覆一次，已與我們無關，債多不愁。）
富利葉轉換
非週期性函數，有富利葉轉換 f(x) -> F(k) 。
如何看出富利葉轉換是一種基底展開？積分就相當於加總。以 eikx 作為基底展開原函數。
捲積 (convolution)
http://mathworld.wolfram.com/Convolution.html
http://mathworld.wolfram.com/ConvolutionTheorem.html
捲積定理的證明 （照定義代即可）
以球諧函數作為基底
原子的量子力學問題 ( 能量本徵值相異者，波函數必正交 )
繞射與晶體結構
原子的假說（原子論的復興）
原子論的復興
反應物與生成物的比例
氣體動力論預測氣體方程式
解釋布朗運動導出出擴散係數
有序的排列與晶體的天然外形
有人用原子的模型想像形成固定特定晶面的理由
佛朗豪斐爾 (平行光) 繞射
什麼是傅氏光學？
利用繞射來了解晶體結構
回想（單、雙）狹縫繞射的反逆性結果
常數函數
δ 函數
常態分佈（高斯）函數
週期性 δ 函數
實驗的 X-ray 晶體繞射/條紋範例
單晶 (斑點)
粉末 (條紋)
繞射實驗的斑點與富利葉轉換
詳細說明（結構因子）
X-射線繞射與原子的週期性排列
與一個散射中心交互作用的結果：
25 個原子時 (2D)
等比級數公式：（1 減公差）分之（首項減末項），如下
Diffraction Patterns of Crystals
NaCl
Ba3W2O9
倒空間
有晶胞週期向量 a1, a2, a3，想建構出 ai . bj = δij 的
雙螺旋
http://163.13.111.54/bio_rev/x-ray_diffraction.htm
蛋白質
胰島素 (Insulin)
第一個被定序出來的蛋白質。但需要結晶，才能用 X-光繞射定結構。（第一個被定出 3D 結構的蛋白質則是肌紅素 myoglobin。）
形成晶體時候的樣子（凡得瓦力）
葉綠體的光合作用系統
這是第一個被長晶出來的膜蛋白質（它是嵌在脂質雙層膜上面）。它是三個相同的單元構成的扁平巨大分子複合體。每個單元都有十幾個蛋白質，共同容納葉綠素及類胡蘿蔔素。 (怎麼會那麼剛好的形狀及大小？)
光合作用的中心在一個很像血紅素帶氧中心的部分，含有 heme 分子
Protien Database (PDB)
AlphaFold 與蛋白質折疊問題
仍有眾多的 蛋白質是沒有辦法長成晶體的。電腦模擬成為重要工具。近年更加上深度學習人工智慧，對己知胺基酸順序，預測蛋白質立體結構。
晶體與幾何
（本節與結晶學有關的圖片，引用自 Marder 所著的 Comdensed Matter Physics 教科書）
晶體為何會形成
週期性是描述晶體的利器
利用對稱性來分類晶體
對稱操作與對稱群
七大晶系與 14 類晶格
32 點群 與 230 空間群
http://newton.ex.ac.uk/research/qsystems/people/goss/symmetry/Stereographs.html
http://newton.ex.ac.uk/research/qsystems/people/goss/symmetry/Solids.html
立體對圖 ( Setreo-pair Graph )
如何看？近視法（交叉）（鬥雞眼）
使用鬥雞眼、把兩個圖看成恰好三個，小心調整焦距把中間那個看清楚（但同時同餘光仍維持是看到三個圖的情況，一開始若不習慣，可用一支筆的輔助來鎖定焦距）。
近視法、交叉視法：看立體對圖時，雙眼視線交會點在圖形的前面；
遠視法、平行視法：看立體對圖時，雙眼視線交會點在圖形的後面。
另一張範例（近視法）
再一張範例，有輔助點的（近視法）
用立體對來看幾種常見的晶體結構
簡單立方
體心
面心最密堆積
六角
六角最密堆積
鑽石
氯化鈉
閃鋅礦
wurzite
http://cst-www.nrl.navy.mil/lattice/struk.jmol/b3.html
Crystallographic Restriction Theorem
五重對稱性不存在的證明
換句話說，是要證明，2p/n 的角度裏，只有 n=2, 3, 4, 6 是可能的對稱操作轉動。
證明的策略：由於轉動是保長的（即長度會是不變的），因此我們想知道某種角度的轉動是不是被允許的對稱操作，只要看會不會造成最鄰近的格子點的距離進一步縮小即可（重合是 OK 的）。
首先，一個值得知道的事實是，滿足週期性對稱的充分必要條件是它構成 Bravais Lattices，也就是 R = ma+ nb ，所有整數 m, n 所構成的 R 的集合（二維的情況）。(Bravais Lattice : A collection of points in which the neighborhood of each point is the same as the neighborhood of every other point under some translation.)
在不失一般性的情況下，我們找出兩個最鄰近的格子點，將連接該兩點的向量叫 a， 以左邊那點為中心，旋轉角度 theta ，則原右手邊的點移走並重合於另一個點（若不重合則創造出一個新的點，則此旋轉就不可能是一個對稱操作）。現在，我們在新點與舊點之間拉一個向量，這個向量也會是一個平移的對稍性操作，我們先來看看它的長度，如果長度比 | a | 還要短，則予盾，因為 | a | 是最近兩點的連線。新的這個向量是 (| a | cos(theta) , | a | sin(theta) ) - (| a |, 0) = ( | a | (1-cos(theta)), | a | cos(theta) )
證明五重旋轉對稱軸無法存在於週期性對稱操作
在所有的格子點中找出兩個最接近的，在不失一般性的情況下，一左一右，拉一條向量，這會是最短可能的週期向量。再來，各自針對兩個點作 2π/n 的正負方向轉動，左手邊的點轉 2π/5， 右手邊的點轉 -2π/5，如此與原先的兩點連線形成一個梯形，這個梯形的斜邊長等於底部長（因為斜邊的點是轉動得到的），至於平行於底邊那個新連線，它的長度是兩個 | a | cos(2π/n) 的和，這個長度要是比 | a | 短，就是予盾了。現在我們注意 cos(x) 在第一象限是一個遞減函數，角度從 0 到 90 度其函數值從 1 遞減到 0。它在 90 度時才會使梯形的頂邊長等於底邊長，此時為 2π/n 的 n=4；而在 60 度時兩點重合，梯形成為正三角形，此時為 2π/n 之 n=6。對於 n=5 而言，頂邊的長度不為零且又比底邊短，故矛盾。
對於 n 大於 6 者，新轉出的點對原位置點所拉出的向量長度比 | a | 小，如此也是矛盾。
我們證明了 n = 5 與 n > 6 者都不可能。
至於 n = 2, 3, 4, 6 是否就一定可能，這就比較簡單，實際作出一個範例即可。
綜合以上，得證。
準晶 ( Quasi-crystal ) （以下圖片取自 Marder, Condensed Matter Physics 教科書）
令人驚異五重對稱結晶
這是怎麼回事？
規則性 卻 無週期 ？
如何用規則的方法造出非週期排列 ? （倍數放大不對稱單元，在反轉其中的單元致使整體不對稱） （例如三倍一變：＋ ＋＋＿ ＋＋＿＋＋＿＿＿＋ ．．．）
一維準週期性系統的例子
先看一個一維的例子，Fibonacci chain ( 參考 1, 2 )，有一種寫下該數列的方法是：
從一條數線上來看，這個數列有或大小兩種不同的間隔，不是 1 就是 t
其中
是恰好有名的 "黃金比例"。
此數列有一個重要的特性叫 deflation rule，意指如果我們寫下此數列任何相鄰兩個數字之間的差，並把 1 換成 t 、把 t 換成兩個數的小數列 t, 1 ，則與原數列一樣。
例如，有一個序列
接著進行
就會得回到
在此介紹此一數列的原因是要找一個蠻有規律性的數列，然而它卻不具有週期性。事實上，這個數列被稱為具有準週期，意味著它在高維度是有週期性的，只是被投影地低維度。
另一種建構的方法：
這個式子到底是什麼？分析觀點：
原式 xn = n + (τ - 1) int (n/τ) ，己知 τ - 1 = 1/τ
把 n 看作橫軸，x 看作縱軸，若只看 xn = n ，斜率 45 度，各 xn+1 - xn 等間隔。 我們關心斜邊上值域點的間隔。
斜率如果是有理數，則必存在 xn / n = p / q ，即週期結構。如果斜率是無理數，就不會有週期性。
現在，想想下式 ：
xn - n = (τ - 1) int (n/τ)
（參考下圖）放在橫軸來看，xn的值，在減去 n 後的，作直角三角形的底，而 n 點對應到的 ( 1/τ) n 的整數點，構成的三角形斜邊有共同的斜率。
在斜率是 1/τ的線上，找垂直寬是 1 的區間帶，恰會有一個整數點，這個點的高度是 int ( ( 1/τ) n ) = int ( n /τ) ，以這個高作餘弦，問一斜率是 1/τ的角，其正弦長是多少，當然就只是簡單地把長度乘上斜率 來得新高度而己，也就是 int (n /τ) times ( 1/τ)，即 ( 1/τ) int ( 1/τ)， 也就是式子中的 (τ - 1) int (n/τ) ，因為 1/τ 恰為 (τ - 1) 。
因此關係式 xn - n = (τ - 1) int (n/τ) 的確重現了(下面) 2D 圖中的橫軸上的 標定 xn
從 2D 來看
從另一角度看
（上圖來源：http://www.jcrystal.com/steffenweber/qc.html）
把一維結構這樣做的好處在於，方便基於其二維是週期性的特性，作 Fourier 轉換 （會用到捲積理論）
潘洛斯鋪磚 (Penrose Tiling)
有名的 Penrose Tiling，是一個以非週期的方式用瓷磚將平面鋪滿的方法。
數學家的頑童心態？最早發表於 " 園藝雜誌" Gardener (1977)
（註：黃金比例 long / short = (long + short) / long ）
非周期 ?
滿足 deflation rule ，在原來的兩種 tiles 上刻出分割線及記號，注意灰色面積與原來的瓦片面積一樣。
上圖 (A) 的與 (B) 各畫上了五條參考線，角度各差 2π/ 5。鋪完整片後，可見寬帶與窄帶兩種長度拼成的序列，五個方向都一樣有。
真實原子排列的情況
在實驗上有觀察到的，有複雜結構的合金具有形變的二十面體（最密堆積如面心及六角最密堆積矽排列方法，每個原子都被十二個原子包圍，若把這十二個原子的中心用直線互連，則形成一個理想二十面體）。一般認為，是各種變形的二十面體實現了在空間中連續排列填滿的最低能量狀態。其中有三度空間的準晶，也有二度的。下圖就是鋁銅鈷合金形成二維準晶的層狀排列。以掃描穿透式顯微鏡 (STM) 記錄到的表原子影像。
具有 12 個頂點的 20 面體 (icosahedron)
具有 20 個頂點的正 12 面體 (dodecahedron)
http://zh.wikipedia.org/zh-tw/%E6%AD%A3%E4%BA%8C%E5%8D%81%E9%9D%A2%E9%AB%94
完美的五角（五重軸）多面體是怎麼堆出來的
Deteministic packing can generate none periodic structure, one example is Penrose tiling.
圖 : big alloy quasicrystal photo (一格 1 mm)
Cluster 模型 有好看易懂的 YouTube 影片(quasicrystal zen magnet) 但勿誤解為必須以 hierachical 方式形成 那樣單元團間孔隙將會過大
關鍵觀念在於："局部對稱性已足夠保證晶體 在五個方向上的成長"
圖 : crystal mophology and miller index (待選)
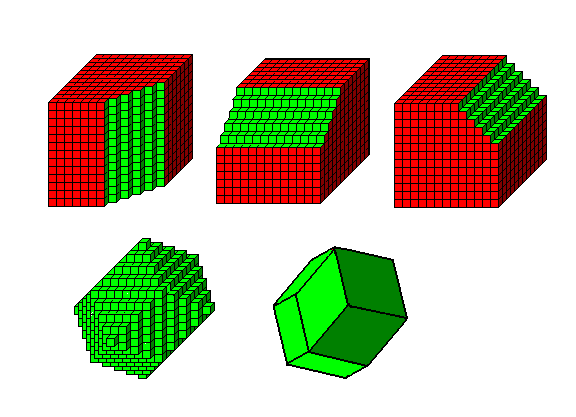
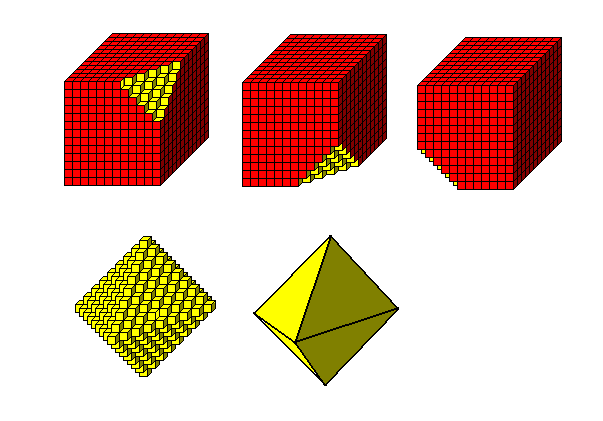
可能的晶面構形（成長越快的那個晶面, 露出越少）
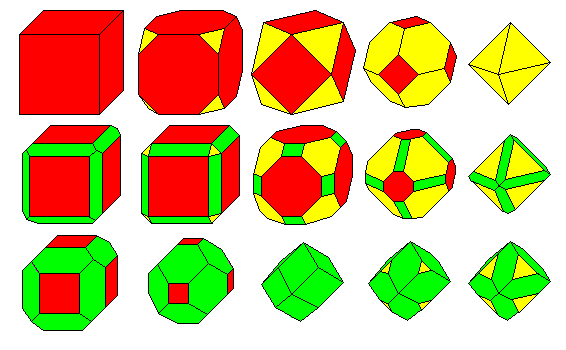
Rhombic tricontadehron
層層套疊
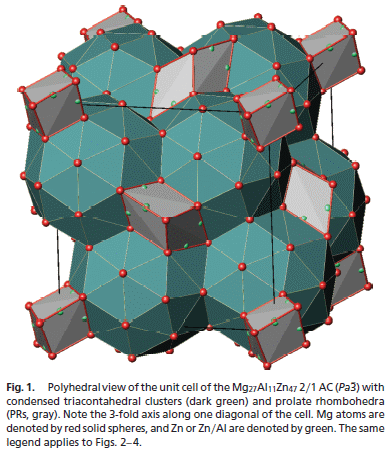
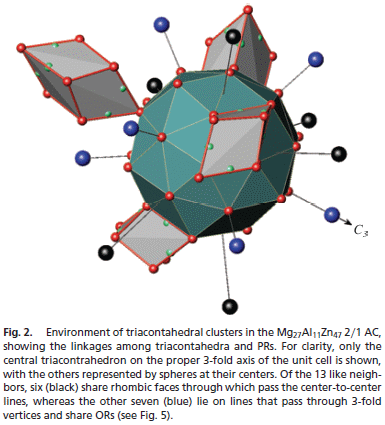
釐清公案所學到的經驗
鐵則還是可以打破的。
倒空間圖 (X-ray 繞射) 與實空間圖像 (電子顯微鏡) 互補不足。
網路資源
QUASIG
http://www.condellpark.com/kd/quasig.htm
Penrose Tilings and Wang Tilings
http://www.valdostamuseum.com/hamsmith/pwtile.html
另一種美麗的 tiling , Hyperbolic Planar Tesselation
http://www.plunk.org/~hatch/HyperbolicTesselations/
2011年諾貝爾化學獎—準晶的發現
http://web1.nsc.gov.tw/fp.aspx?ctNode=1104&xItem=14728&mp=1
Youtube 上的玩具示範
http://www.youtube.com/watch?v=J6iAvYgLAC4
軟體
http://www.jcrystal.com/steffenweber/qc.html
