能量 與 第一定律

 

溫度之外，另一個 key concept 是 能量

能量及能量轉移在有溫度的情況下，有什麼特性？

能量的變化如何改變？（作功　升溫　量子態）

從一份熱可以做多少功？

 

一些名詞的定義

熱平衡的系統

系統：我們要研究的宇宙的一部分

熱平衡： 巨觀量不再隨時間改變

 

狀態函數

狀態 ：(各)巨觀的可觀量與演變的歷程 (或路徑) 無關

狀態 (v.2)：與歷程 (或路徑) 無關的物性

我們下面將會具體說明　為何功與熱都不是狀態　

狀態函數：該可觀量 (描述狀態的自變數)，在系統平衡後，與時間無關。

狀態函數：有那些？（溫度、壓力）

 

問題思考

兩個系統有某個狀態函數一樣，有什麼意義？

兩個系統有很多個狀態函數一樣，有什麼意義？

兩個系統所有狀態函數都一樣，有什麼意義？

狀態函數是有限個還是無限個？

回答了上述問題，又到底有什麼意義？

 

以下什麼比較接近狀態函數？

姓名？八字？學歷？年齡？(FB)感情狀態？

 

時間是微觀量還是巨觀量？

那空間呢？

 

定義狀態函數的目的：描繪能量

例如，層架上的花瓶與位能（只有高度的不同，其他沒任何相異，低層落下沒事而高層落下則摔破）。

 

狀態函數的用法

描述系統

 

狀態函數的數學處理

描述狀態的一組參數 x = ( x1, x2, ... ) ，構成狀態函數 f(x) （注意這些描述系統的參數本身也是狀態函數，是我們之後想要組合出各種更複雜的狀態函數，才用 f(x) ）

此一系統的參數從 xi 變化至 xf

Δf = ∫xixf  df = f(xf) - f(xi)

 

Ex 1.1 三條不同路徑的函數積分值 （見下圖）

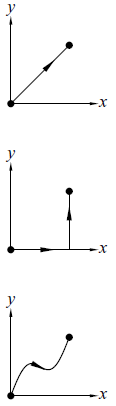
系統 由 x 與 y 兩個狀態函數描述

假設 f = x y

則 df = x dy + y dx

Δf = xy |xfxi=> 只跟初態與末態函數值有關。

另外假設 dg = y dx （ dg 是一個 inexact  differential）

則 Δg = ∫ ... ...

見 (11.4)、(11.5) 式，已可見不同（不用再看第三種路徑了） 。

 

重點：狀態函數一定是全微分的形態，否則無法成為狀態函數。

 

 

熱即能量

歷史故事：熱為何物？

熱素

鑽磨砲身發熱不絕

 

熱功當量 (mechanical equivalent of heat) 的測量：焦耳與梅爾

 

西遊記火焰山的溫度；世界紀錄最大支的溫度計的質疑

背著溫度計去蜜月旅行的（疑似）肖仔

 

（牛頓–米在轉動問題中是力矩，等效於焦耳的討論，見 http://en.wikipedia.org/wiki/Joule）

 

 

熱力學第一定律

熱力學第一定律：能量守恆，且熱與功皆為能量之形式

一個系統的內能 U，是其內部自由度之能量的總和。U 是狀態函數。

 

ΔU = ΔQ + ΔW

 

ΔU ：系統的內能變化

ΔQ：加到系統的熱

ΔW：對系統作的功

 

問題：系統的內能，真的只能透過加熱與作功這兩種途徑嗎？

問題：一保險箱內置炸藥，密閉後引爆之，內能有沒有改變？

 

對於微小變化

d U = δQ + δW

或

d U = đ Q +đ W

其中đ Q 和 đ W 都不是 exact differential，也就是 inexact differential

（為什麼？） （Hint：功、熱都是能，而能量守恆。）

 

đW ≡ f dx

因此對氣體，有

đW =  - p dV

其中負號來自 "定" 對氣體系統 "壓縮" 是作 "正功" ，由以上形式，如此足見功不是狀態函數。

 

思考：熱力學方程式中所出現的量，是狀態函數或不是，有什麼重要性嗎？

 

 

 

比熱

我們現在想更深入了解，加入熱是如何改變 "氣體的" 內能。

我們將會看到，從第一定律的框架下，定容比熱與定壓比熱的關係。

作法：dQ = dU + p dV 已知，再代入 dU 與 T、V 的關係，使我們可得 dQ 與 dT、dV 的關係。

 

對氣體，一般 (in general) 而言，U = U(T, V) 

（為什麼這句話是對的？不可以再有更多其他的自變數嗎？） （試回憶理想氣體方程式，總共也才幾個獨立變數而已。）

 

諸多偏微分關係，詳見課本 . . .

dU = (∂U / ∂T )V dT + (∂U / ∂V )T dV

由前面的  dU = d Q + d W 又 dW =  - p dV，則

dQ = dU + p dV

將上式 dU 的完整偏微分形式代入其中，並同除以 dT，得

dQ / dT = (∂U / ∂T )V + [ (∂U / ∂V )T + p ] ( dV / dT )

之前曾定義

CV ≡ (∂Q / ∂T )V

則基於上面 dQ / dT 形式，第二項無貢獻，故有

CV = (∂U / ∂T )V

至於 Cp 則為

Cp ≡ (∂Q / ∂T )p

= { (∂U / ∂T )V + [ (∂U / ∂V )T + p ] ( dV / dT ) }p

= (∂U / ∂T )V + [ (∂U / ∂V )T + p ] ( ∂V / ∂T )p

= CV + [ (∂U / ∂V )T + p ] ( ∂V / ∂T )p

 

Cp- CV  = [ (∂U / ∂V )T + p ] ( ∂V / ∂T )p

 

我們有時希望描述每莫耳熱容或單位質量熱容，故定比熱

cV = CV / M

cp = Cp / M

 

 

Ex 11.2  理想單原子氣體的熱容

每莫耳理想單原子氣體 U = 3/2 RT ，只與溫度有關，故

( ∂U / ∂V )T = 0

再用上了每莫耳分子 pV = RT

，即 V = RT/p ，故

( ∂V / ∂T )p = R/p

由前有之 Cp- CV  = [ (∂U / ∂V )T + p ] ( ∂V / ∂T )p = [ 0 + p ] R/p = R

再由 U = 3/2 RT ，而有 CV  = (∂U / ∂T )V = 3/2 R ，則 Cp  = 5/2 R

 

Ex 11.3 dU = CV dT 普遍成立嗎？

（只有理想氣體才對，詳見課本）

 

一個有用的量， adiabatic index (exponent) ，之後會用到

γ = Cp / CV

 

Ex 11.4 理想氣體的 γ值計算

 

Ex 11.5 理想氣體的 (i) 單位質量內能與 (ii) 單位體積內能 計算