注意函數與方程式定義上的差別
函數:是一種映射,只要不是一對多(像足在只要不是一對多(像是一對一、多對一皆可)
方程式:簡單的講就是有等號的式子。
如果問題中只有一個自變數(也就是一維的問題),那這通常被叫做是函數求根。
方程式求解與函數求根的問題有時在形式上很像,例如像 f(x) = 0 這種樣子。 要解 f(x) = 0 這條方程式,就相當於對函數 f(x) 求根,不過定義與陳述方式上的不同(方程式求解、函數求根)大家還是要注意一下。
如果是多個變數與多條方程式,則可用向量形式簡寫為 f(x) = 0 (這裏粗體字代表向量符號),則問題的複雜度就高銀多了。
隱函數理論
N 個獨立的自變數有希望可以一次滿足 N 條方程式。注意,只是有希望,因為非線性方程組有可能根本無解。(請複習回想一下什麼是線性,又線性方程組其有解無解如何判定。)
N 個獨立變數所滿足 N 條方程式的解 "一般而言" 會是一個個(即一組組)獨立點而沒有連在一起的(反例:單一條方程式 f(x) = x12 + x22 = 0 的解在空間中形成一個圓)。除非剛好遇到相當特殊的簡併狀況,才會有一整條連續解出現。
f(x) = 0 與 f(x) = 0 雖然形式很像,但難度有天壤之別,主要是差在,想求解前者,可以用求函數值之正負用頭尾逼近的方法,然而一旦是高維度,解就沒有辦法光靠求函數值就來作判斷得到了。因此,函數求根(或一般代數方程式,即不含微積分的方程式)需要透過有效的演算法來找出,而且都是需要藉由反覆迭代的方法(只有線性的問題才可能不需要反覆迭代)。
不過,為簡單入手起見,我們先從一維的問題開始講。
儘可能對想求根的函數有基本的認識
作者強調對於一維問題,一定要儘可能先對根的分佈有一點了解。如此萬一有找到錯的根、或是因為本來在那裏就沒有根所以沒找到,抑或是初始猜測值離太遠而沒有找到,遇到上述狀況才會有助於進一步處理與判斷。作者引用 Hamming 的格言說:" The purpose of computing is insight, not numbers." (Richard W. Hamming 是對電腦科學與通訊貢獻很多的數學家,也寫了多本受好評的書,其中一本是:Numerical methods for scientists and engineers。)
初始猜測很重要,會影響到是否找得到根(尤其是在多維度的問題),以及所花的時間。作者提醒讀者,在處理一維問題時,應先把解包圍起來(bracket the roots) ,才使用迭代方法去搜尋根。
有人可能會問,若自變數的範圍是 負無限到正無限,怎麼可能包圍得完?這也就更突顯了對問題本質先行了解的重要,另外,對於真實科學或工程應用上的問題,自變數 x 的範圍往往已經從問題的本質中就已經是確定或限定的了。
作圖預覽法
課本提了供了一種只需要文字螢幕的終端機就可以畫出函數在所給定上下限範圍的副程式,叫 scrsho (screen show)。它並且會調節 y 軸的尺度及上下限來確保全部的函數圖形(在該次所選定的範圍內)都可以看得到。
副程式 scrsho
SUBROUTINE scrsho(fx)
INTEGER ISCR,JSCR
REAL fx
EXTERNAL fx
PARAMETER (ISCR=60,JSCR=21) Number of horizontal and vertical positions in display.
For interactive CRT terminal use. Produce a crude graph of the function fx over the
prompted-for interval x1,x2. Query for another plot until the user signals satisfaction.
INTEGER i,j,jz
REAL dx,dyj,x,x1,x2,ybig,ysml,y(ISCR)
CHARACTER*1 scr(ISCR,JSCR),blank,zero,yy,xx,ff
注意要點:函數的具體定義是要在上一層先定好,有些 compiler 有支援直接用
fx(x) = x**2 + 3*x + 2.0
寫在主程式裏這樣的方式。
有些 compiler 不支援上述方式,則請改用標準作法,作法是自行定義 function,以 scrsho_main.f 為例(要請大家特別注意的地方以彩色標出):
program scrsho_main
real fx
external fx
call scrsho(fx)
end
function fx(a)
real fx, a
fx = a**2
end
再下 gfortran -o scrsho_main.x scrsho_main.f scrsho.f 即可產生執行檔 scrsho_main.x
對於一維的連續函數,我們可以利用上述特性寫一個程式來找出根是會在那一些區間,但首先讓我們看一下幾種找根時會遇到的狀況,這些例子提醒我們在設計以包圍的方法來根的時候要特別小心:
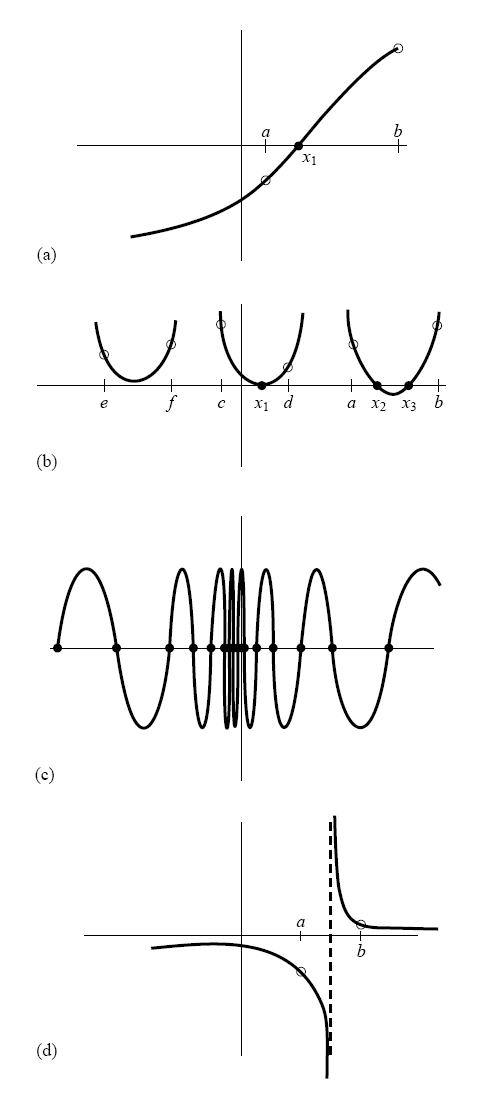
其中 (a) 是很標準的理想狀況、(b) 取的範圍都沒有變號的,但除了第一段是真的沒有根之外,第二段是重根設沒有偵測到,第三段是兩個鄰近的根沒有偵測到;(c) 有可能函數之解的分佈很特殊,在某些區域會有很密集的根;(d) 即便是有變號,也有可能沒有根,像 f(x) = 1/(x-c) 這樣的函數。
作者再次提醒大家,如果你對待求根的函數一無所知(或者說完全沒有一點預作的評估),則並沒有什麼很確定的包圍策略可以用。一個例子是課本 (3.0.1) 式
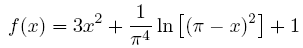
它的兩個根是
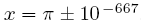
也就是說,若用包圍法,那這個函數會變號在極小極小的範圍裏。
作者也提到,不同於另一章專門找函數極小的章節中所用的 "向下找最低點" 的方法,這種方法並不能在求根時候用(因為有人可能會認為,我們可以把找 f(x) 變號這件事改成找 [f(x)]2 ,反正它最小也就是零,但是只要 f(x) 中有斜率是零的極值, "向下找最低點" 的方法就無法百分之百生效,因為它是靠斜率指引函數值是要向上或向下。 然而,至少,如果我們有心理準備,則這種 "向下找最低點直到變號 " 也是可以作為開始找尋方法,對正負無限遠兩邊函數值不同號的求根蠻有用的。
包圍的方法,課本提供了兩個副程式,
副程式 zbrac
SUBROUTINE zbrac(func,x1,x2,succes)
INTEGER NTRY
REAL x1,x2,func,FACTOR
EXTERNAL func
PARAMETER (FACTOR=1.6,NTRY=50)
Given a function func and an initial guessed range x1 to x2, the routine expands the range
geometrically until a root is bracketed by the returned values x1 and x2 (in which case
succes returns as .true.) or until the range becomes unacceptably large (in which case
succes returns as .false.).
INTEGER j
REAL f1,f2
LOGICAL succes
給初始邊界 x1、x2 ,此副程式自動向外擴張邊界直到包圍到左右邊一正一負(即確定至少有一個根)為止,或是擴張到非常大的範圍仍找不到也會放棄。 基本上這是向外擴大範圍找尋。
副程式 zbrak
SUBROUTINE zbrak(fx,x1,x2,n,xb1,xb2,nb)
INTEGER n,nb
REAL x1,x2,xb1(nb),xb2(nb),fx
EXTERNAL fx
Given a function fx defined on the interval from x1-x2 subdivide the interval into n equally
spaced segments, and search for zero crossings of the function. nb is input as the maximum
number of roots sought, and is reset to the number of bracketing pairs xb1(1:nb),
xb2(1:nb) that are found.
INTEGER i,nbb
REAL dx,fc,fp,x
使用 zbrak 的方法是,使用者給定範圍 x1、x2,以及要均符分割幾等分 n,副程式會逐一檢查每個 n 等分區間是否被一正一負的函數值包圍,有找到的區間以 xb1、xb2 輸出,共 nb 個,但 nb 初始值以預期要找的根之數目的上限值傳入。 提醒,n 可以用很大。
一旦知道了包圍住根的範圍,就有多種演算法可以選擇,各有不同的收斂速度,越保險的就越慢。在此介紹一個最保險的方法,就是二分法。
二分法找根的基本策略很簡單,就是針對函數已有變號的範圍,取其中點求函數值,此值非正即負,則新的較小(僅原來之一半大小)之範圍就可次被求得,如此反覆做下去,可在所需的容忍度範圍內找到所要的根。
函式 rtbis (root bisection 之意)
FUNCTION rtbis(func,x1,x2,xacc)
INTEGER JMAX
REAL rtbis,x1,x2,xacc,func
EXTERNAL func
PARAMETER (JMAX=40) Maximum allowed number of bisections.
Using bisection, find the root of a function func known to lie between x1 and x2. The
root, returned as rtbis, will be refined until its accuracy is ±xacc.
INTEGER j
REAL dx,f,fmid,xmid
在已經知道 x1、x2 之間有一個根的情況下,反覆以二分法縮小範圍,直到在所給的誤差容忍度之間。
請注意 rtbis 是當函數(函式)用,而非副程式。
寫一個主程式來使用 rtbis 函式之範例:
program rtbis_main
real func, rtbis, x1, x2, xacc
external func, rtbis
write (*,*) 'What is the range x1 and x2 and accuracy ?'
read (*,*) x1, x2, xacc
write (*,*) 'A root is at ', rtbis(func,x1,x2,xacc),
& ' with accuracy ', xacc
end
function func(x)
real func, x
func = x**3
end

![]()
![]()