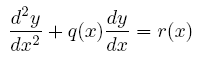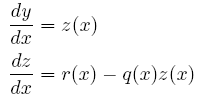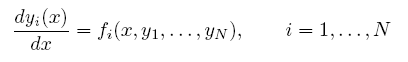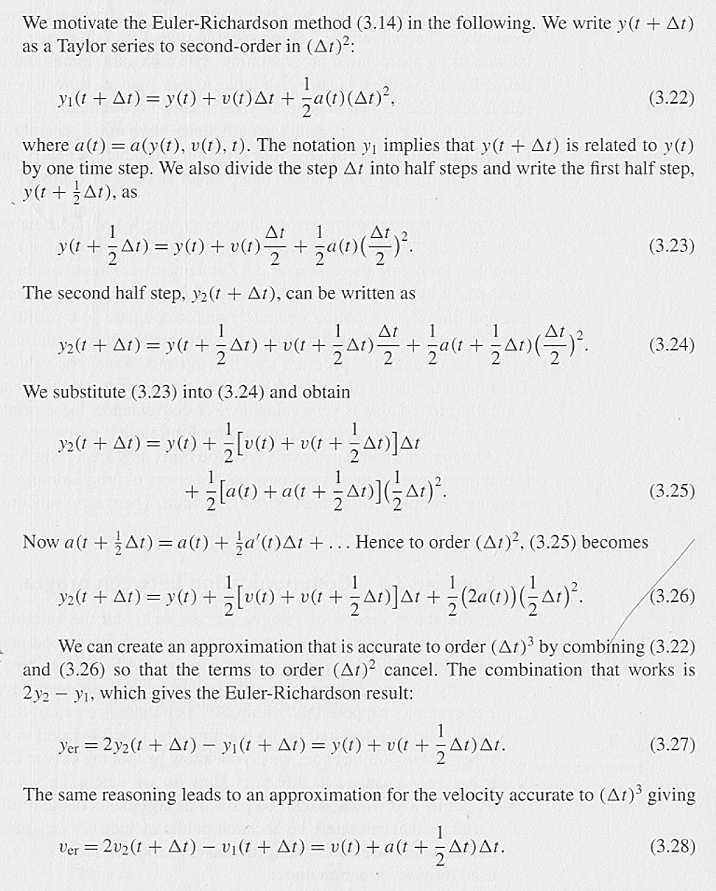常微分程求解：基本問題剖析，奧依勒法、泰勒展開與高階方法
微分方程式
微分方程式是方程式，所以有等號，並且待求解的未知函數有以導數（對函數的自變數微分）出現在式子中者，即為微分方程式。（如果完全沒有微分符號出現在式子中的就不算）
在微分方程式中，又分：
常微分方程式 (Ordinary Differential Equation)
只有一個變數
偏微分方程式 (Partial Differential Equation)
有多於一個自變數
處理高階微分方程的(數值)方法
一個常微分方程式的一般形如下：
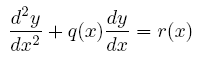
透過令一階導數 y'(x) = z(x)，就可以把原本一個二階的 ODE 化成兩個聯立的一階之 ODE，如下：
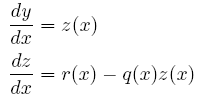
一個二階 ODE 原本就需要兩個條件來決定兩個待定的積分常數，而兩個一階的 ODE 則變各需一個，也是兩個，因此剛好，完全沒有改變原本該有之解的本質。同理推之，任何 n 階 ODE 皆可等效地轉換為 n 個一階的 ODE。因此，我們所需要關心的是，像具有以下這種 通式形式的一階 ODE 該如何求其數值解 yi(x)，注意 y1、y2、...、yN 分別代表原待求函數 y(x)、y'(x)、...、y(N-1)(x) 等，一共有 N 個，要同時滿足下列 N 條方程式：
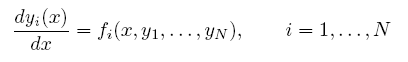
注意等號右手邊的 fi 可以是各階導數 yi 的顯函數。
Euler 演算法
一階微分方程式的程式
最一般形式的一階微分方程式，是如下的形式：
dy/dx = f(x,y)
其中 f(x,y) 可次是任何以 x, y 為自變數的顯函數。在微分方程式的問題中，f(x,y) 為所給定的已知，而 y(x) 則是未知且希望求得的解。
我們要如何求解 y(x) ？
Euler （奧依勒）演算法
在 Δx → 0 的情形下 Δy/Δx = dy/dx = f(x,y)，也就是說Δy = f(x,y)Δx。
把 x 分成許多等間隔的小單位，即Δy ≡ yn+1 -yn、Δx ≡ xn+1 - xn，則上式成為
yn+1 - yn = f(xn,yn)Δx，也就是說
yn+1 = yn + f(xn,yn)Δx
上式就是 Euler 演算法，它告訴我們只要知道第 n 格的 y(x) 值 yn，就可以算得下一格的 y(x) 值 yn+1， 故只要知道 y(x) 在某個 x0 處的起始值 y(x0)
（在不參考任何資料的情況下，要能推導出 Euler 演算法的公式）
高階（誤差項）的方法
從泰勒展開式的角度來看，
y(x+Δx) = y(x) + y'(x)Δx + O(Δx2)
也就是說，
y(x+Δx) = y(x) + f(x,y)Δx + O(Δx2)
這是所謂的一階方法，它最高次的精確項是Δx 的一次方項，後面的 O(Δx2) 代表所有的誤差都在Δx 的二次方（含）以上。
像 Euler 演算法這樣的一階方法是有缺點的，簡單地說，它的準確度不夠。或許你會想，Δx 取小一點就會比較精確，比方說，取為原來的十分之一大小，然而，這也意味著同一個問題的的切割區間數多了十倍，運算次數就要多十倍，如比進位誤差就會很大。（所謂的進位誤差成截斷誤差，是指由於電腦中只能保留有限個位數，因此數據的最後一位在每一次進行運算時便不免有誤差，且運算次數多時，誤差還會被進到前面的位數。）
你或許又想，即然如此，那就做更高次的好了，也就是把Δx2 甚至更高次項的公式也寫下來，不就很精準了嗎？但是不行，在使用電腦做數值計算時，我們是絕對不能把兩個很小的數值乘在一起的，因為電腦內沒有足夠的位數來表示它們乘積的結果，這樣做所導致的誤差是災難性的。
半步方法
利用泰勒展開式，但只在半步展開的策略，可以幫助我們建立更精準的高階方法，而卻一樣只需要用到Δx 的一次方。 以下是 Gould 與 Tobochnick 的An Introduction to Computer Simulation Methods 教科書附錄中所介紹之兩種的方法的比較，其中 Euler algorithm 是一階方法，而 Euler-Richardson algorithm 則是二階方法，也就是說，表示法仍只是Δx 的一次方，而誤差的部分確是三階（含）或以上的 O(Δx3)，這是怎麼辦到的，讓我們看以下的推導：
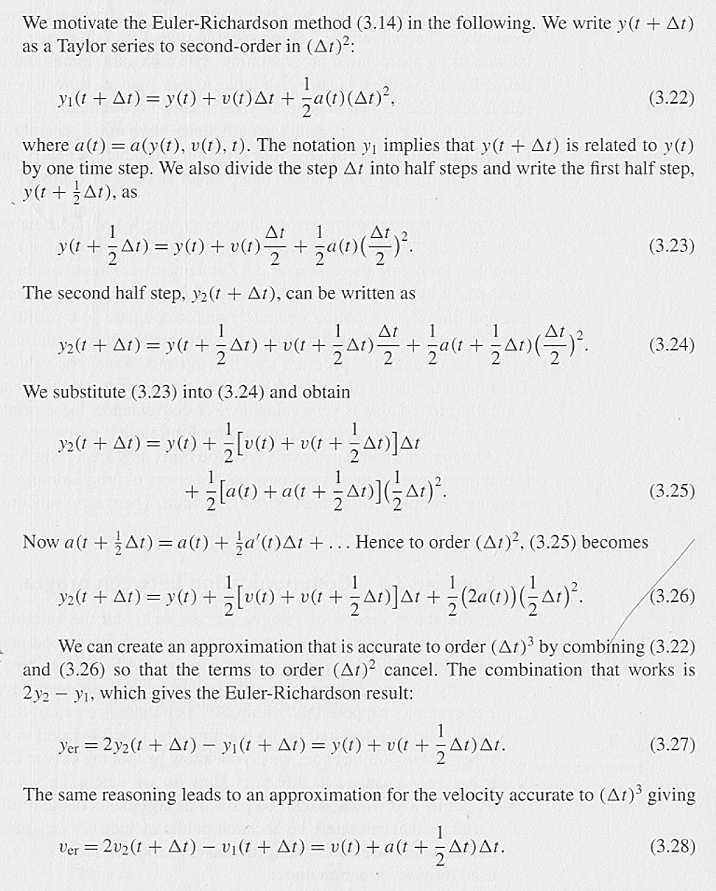
我們在這裏學到的經驗是，透過求值在半步的斜率，回到出發點用以推進積分的下一整步步（解微分的問題事實上這相當於是積分），如此 "以退為進" 的方法， 可以大幅提高精確度。其實，除了這個可達二階精確度的方法外，更高階精確度的方法也是存在，並且是利用類似的策略所推導出來的。
本單元沒有副程式
