微分方程問題的求解是一定會涉及到待定常數的,最高階導數是幾階就會有幾個。上一單元的常微分程求解,我們學到了處理所謂初始值問題的方法,也就是說,一開始就己經知道那些初始條件,因此我們就一直代下一步、再下一步,直到把自變數的範圍做完為止,整個過程算是蠻直接的。例如炮彈軌跡,全由一開始的初速率及炮口角度所決定,就是一種典型的初始值問題。不管自變數是時間還是空間,初始值類型的問題一開始就提供給各個(高階轉化來的)一階微分方程式足夠的初始值,讓積分可以一步一步進行下去。
但真實世界所要處理的的微分方程,也有一些其條件不全是在自變數開始積分的那一頭就決定的。例如,液體流動是被局限在一個管子之中,抑或是像弦的振盪仍有被固定在兩邊。
對於單一個自變數的問題而言,邊界條件只發生在起點與終點,因此才有兩點邊界條件問題這樣的名稱。
邊界條件不只在空間座標會發生,時間座標也會,比方說所要解決的問題,是利用火炮炮去射擊擊中某個動態的目標,而要求炮彈在某時刻飛抵某特定位置,然後我們要問初速度是多少,飛行的軌跡會怎樣。
我們所要求解的高階常微分方程式,仍然是表示成多個(在此 N個)一階導數的式子:
dyi(x)/dx = gi(x,y1,y2,...,yN)
這裏 i = 1, ...,N ,但 N 個邊界條件有 n1 個在左邊 x1 點、n2 個在右邊 x2 點(n1 + n2 = N),分別是以約制條件方程式(constraint equations)的形式寫下:
B1j(x1,y1,y2,...,yN) = 0 , 其中 j = 1,2,...,n1
B2k(x2,y1,y2,...,yN) = 0 , 其中 k =1,2,...,n2
以上定義了我們在本章所要求解的問題。
射擊法的想法
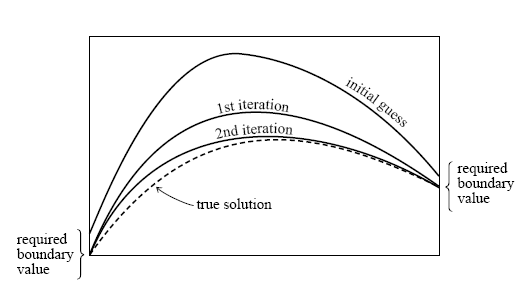
既然在進行 Euler 或 R-K 方法時所需的初始條件沒辦法知道,那麼,如何開始進行?彈道試射提供我們一個點子,在火炮射擊時,未必能在一開始就幸運擊中目標,但我們可藉由觀察彈著點來提供下一發如何修正的資訊,以提昇命中機會。射搫觀念被用在以既有的初始問題方法來解決邊界值問題。以下圖示清楚地說明此一想法:
從出發點左側,所有能用上的邊界條件(剛好也可作為初始條件)都使用之外,不足的部分就先用猜的,如此就可以發動 "嘗試性" 的一步步推進求解。
這裏列出了三次的嘗試,結果的確一次比一次更接近所要的邊界條件值。至於要怎樣讓程式可以學會或自動地越做越正確,則是射擊法的另一個重點,我們在下一個單元會詳細說明。
很明顯地,解兩點邊界值問題所費的電腦運算量會比初始值問題多得多,因為每一條曲線都相當於是一次完整的 rkdumb 或 odeint 呼叫。
放鬆法的想法
另一大類的方法是放鬆法(relaxation methods),圖示如下:
詳細的介紹以及與射擊法的比較,請見課本。對於無法確定用那一種方法比較好的問題,作者建議先射擊、再放輕鬆(雙關語幽默)。