(簡化版:logistic.f)
補充:範例程式中的繪圖指令
pgmove(x,y): 將畫筆移動到 (x,y) 的位置
pgdraw(x,y): 畫筆從目前的位置,畫直線到 (x,y)
pgeras:清除畫面
從幾何作圖的角度來看固定點分佈與數量上(隨 r)的變化
透過一系列作圖可呈現。
非線性動力學以及混沌現象模擬
Nonlinear Dynamical System
一般按英語字面意義翻譯作 "非線性動力學系統",也很常見。其實在這裏的 dynamical 意指系統的狀態時時可以改變,其用法比較像是 DRAM (Dynamical Random Access Memory) 動態隨機存取記憶體,Dynamical Memory Allocation 動態記憶體配置,是 "動態" 的意思,因此 Nonlinear Dynamical System 應稱作是 "非線性動態系統" 才更不易引起誤解。當然,在物理學的範疇中有很多的力學系統也是動態系統,因此針對那些系統以 "非線性動力學系統" 稱之也沒錯,只是這樣對於其他非機械或非力學的系統,如動態的電路訊號變化或動態的人口變化,這名稱就有一點怪怪的了。
什麼是複雜?什麼是簡單?
複雜與簡單雖然只是兩個不具精確物理意義的形容詞,但在這裏至少有一個大家應該都能接受的區分,就是一個現象有沒有週期性。有週期性的現象,預測起來比較簡單,像日昇日落、春夏秋冬;而沒有週期性的現象,諸如氣象變化、股市脹跌。
一個現象會複雜,會令我們無法預測,難到都是因為系統構成的元件很多而個自之間的交互作用又複雜,像封閉容器中所有氣體分子的動向那樣嗎?並不盡然,一個只具有相當小自由度的,服從一個簡單但卻是非線性的公式來變化(演進),也可以產生複雜到無法預測其週期的情況,在物理的現象中我們稱為是混沌現象。
註:混沌一辭很早就有,但與現今用於科學領域上的不一樣,像是小孩子讀的《幼學瓊林》中有 "混沌初開,乾坤始奠,氣之輕清,上浮者為天;氣之重濁,下凝者為地"。文言文中的混沌並不是物理名詞,它主要是要描述宇宙的 "無結構性" 。 另有人引述為“混沌初開,乾坤始奠,輕清者上浮而為天,重濁者下凝而為地”
現在翻譯作混沌(Chaos)的英文原意是混亂,氣象學家勞倫斯用混沌理論,是用來描述僅有些微之差的初始條件就會導致後續的系統狀態有極大的不同,就像是所謂的蝴蝶效應(請見維基百科)那樣。
有些東西的本質本來就是隨機性的,如擲一個骰子會不會出現六點這件事情。並不因為初始條件的些微不同而有異,就不是在這裏所謂的複雜了。
一個簡單的非線性動態系統:一維 logistic 映射
生物族群個體總數 population 與世代的關係
Pn+1 = Pn ( a + bPn )
提出 a 係數後變為 a Pn [ 1 + (b/a) Pn ] ,再變換變數 x = (b/a)Pn 後則原式簡化成為 (a2/b) xn ( 1+ xn ) ,若把 a2/b 再改為 4r 則有 logistic map
Logistic map 的定義
一連串 x |-> x' 、 x' |-> x'' 的映射,每次得到的結果又作為下一輪的術輸入值,其中第 n 次與第 n+1 次具有以下關係:
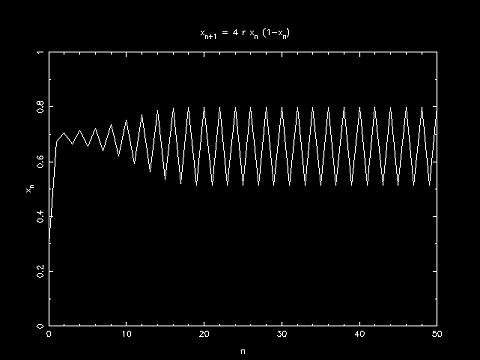
xn+1 := 4r xn (1-xn)
提示:若是寫成程式,就只須要寫一行 x = 4 * r * x * (1-x) 。
非線性的物理意義
讓我們先回想一下化學反應速率與反應物種濃度的問題。假設速率決定步驟是 A + B → AB,則正向反應速率正比於個別反應物濃度 [A] 與 [B] 的相乘 [A][B],又,如果決定步驟是 A + B + B → AB2,則正向反應速率正比於 [A][B]2。 我們都可以理解這是因為要形成產物,(以後者為例)需要三個東西碰在一起,因此有 [A]、[B]、[B] 密度相乘來反映出機率。
假設食物充足等環境因素使然,繁殖率與前一世代的數量呈正比,則式子中會有 x 一次方項;另外,昆蟲疾病的傳染,會經由兩個個體的接觸,如此有了- x2 項,如此就有了
xn+1 = 4r xn ( 1 - xn )
做做看,如果是 x ( a - x ) ,其中 a 是不等於一的某一個同定常數(也就是說上式的 x 的 - x2 並不一定是要相同比例),如此更合理,則結果會如何?(這樣的壞處是沒有歸一化,x 的值的範圍不被局限在 0 到 1 之間。)說明:以 a x + b x2 為例,可轉化為 a (1 + c x) x ,(其中 c = b / a) ,再進一步變成 a/c (1 + cx) cx,最後把 cx 令為最後的 x ,就有 x(1+x) 的形式了。
我們也可以從另一個角度來了解非線性項,若 x 是夠小的值,則現象可次包含高次的效應,而表示成汲級數展開(像泰勒展開式那樣),因此二次或更高次的效應之出現是相當自然的。
程式習作:畫出 Logistic Map 之 x 對 n 的作圖
蟲口隨世代作圖
觀察到:
(1) 進入了叫固定點 (fixed point) 的穩定狀態(與初始蟲口值無關)
(2) 有些(較大的)r 導致會有兩個固定點
(簡化版:logistic.f)
補充:範例程式中的繪圖指令
pgmove(x,y): 將畫筆移動到 (x,y) 的位置
pgdraw(x,y): 畫筆從目前的位置,畫直線到 (x,y)
pgeras:清除畫面
從幾何作圖的角度來看固定點分佈與數量上(隨 r)的變化
透過一系列作圖可呈現。
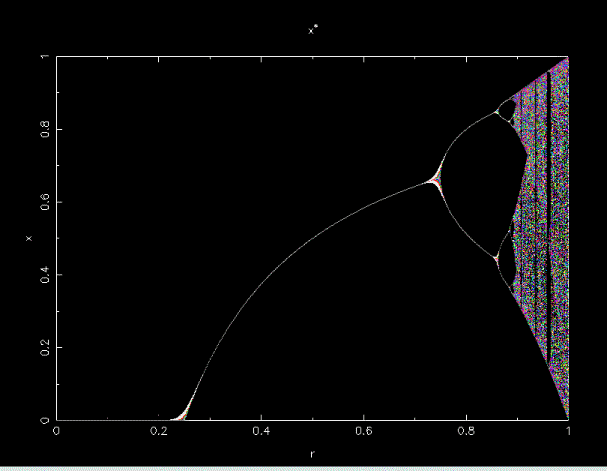
範例程式技巧分析:
隨世代的不同而變化,以不同的顏色表示。將 n_gen 分為 若干段, 第一段不顯色(背景色),剩下者確保 n_gen 輪滿也不會再使用到背景色。(你可以試試世代數 50 到 500 來感受一下)
分叉圖的結構:碎形
放大某一小範圍的 r 來看,我們會見到重覆出現的類似結構。
思考:這是為什麼?
bif_enlarge.f
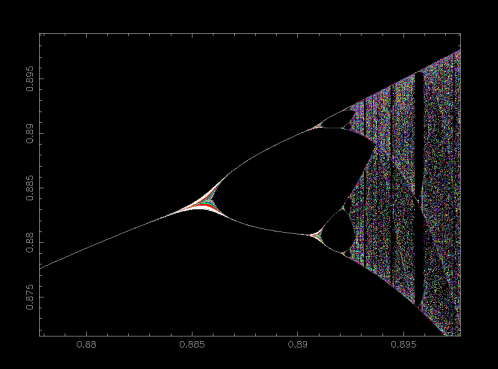
範例程式技巧分析:
pgband 是功能強大的滑鼠游標定位函式,每當運算,就會等待左鍵或是鍵盤敲入,一有動作,就會記錄觸發位置及按鍵字元,供之後使用。 示範如下:
write (*,*) 'Now choose a range to enlarge using mouse pointer.'
write (*,*)
idummy = pgband (0, 1, 0.5, 0.5, x_pos, y_pos, CH)
x1 = x_pos
y1= y_pos
idummy = pgband (2, 1, x1, y1, x_pos, y_pos, CH)
x2 = x_pos
y2 = y_posif (x1.gt.x2) then
temp = x1
x1 = x2
x2 = temp
endif
if (y1.gt.y2) then
temp = y1
y1 = y2
y2 = temp
endif更多細節見 線上手冊
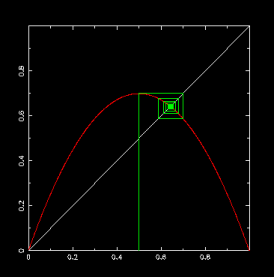
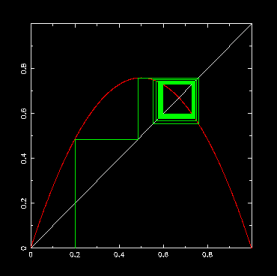
為什麼分叉會發生?從函數的圖形來了解
Logistic Map 如果寫成一個實數形式,其函數圖形就會一個開口向下的拋物線(下圖紅線),而其 r 就代表拋物線的曲率。世代演化一步步迭代的動作,在圖上可用一系列垂直線水平線的對應來呈現,每當有 x 值時,作一次垂直線把 x 對到函數圖線上,其高度是 y 值,接著作一次水平線對到 y=x 對角線上,此位置 y 的值會與 x 的值一樣,則再作一次垂直線觸及函數線,就相當於將代入 x 所得到的 y 再一次令成 x 再代入函數去得 y,如此循環下去,可逼近到固定點。
探討函數與對角線交會處之斜率與分叉的關係
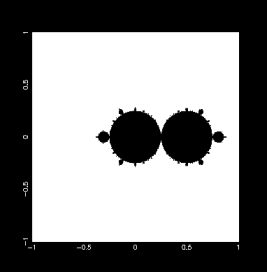
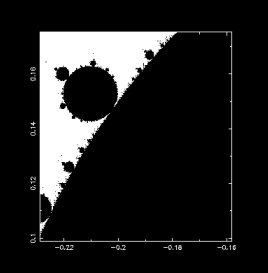
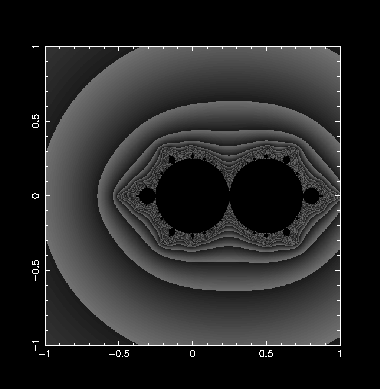
複數 r 的 Logistic Map 與碎形
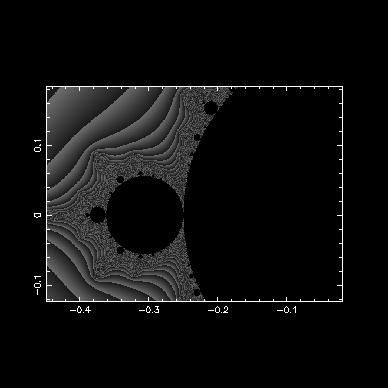
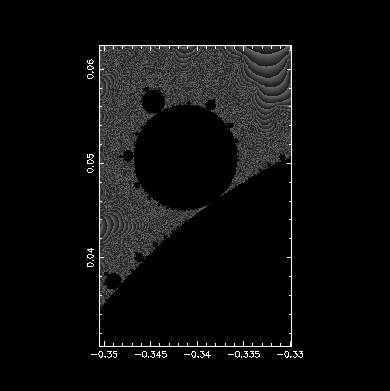
匹茲堡大學數學系的混沌課網頁(有混沌在很多不同領域的應用)
http://pear.math.pitt.edu/mathzilla/Examples/chaos/index.html
混沌藝廊
http://www-chaos.umd.edu/gallery.html
ICM 2006 Benoit Mandelbrot 碎形藝術競賽
http://www.fractalartcontests.com/2006/