波動光學
干涉現象
波動的光
惠更斯是最早先提出可令人信服之光的波動理論的人 (1678) ,雖不如馬克斯威爾方程式來得完整,但卻可用簡單的作法說明反射、折射現象,以及闡明折射率的物理意義。因此值得我們來了解一下。
惠更斯原理
波前上的每一點均可視為球面子波的點源波,經過一段時間 t 之後,波前的新位置將為這些子波的切面位置。
折射定律
不同介質中光速不同,但它們是來自同一道光因此頻率相同,如此則波長不同,有以下關係
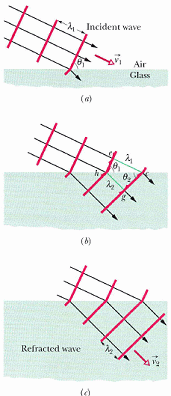
v1 / v2 = λ1 / λ2
上圖中之 三角形 的 角 ceh 與 角 hgc 是直角(因為行進方向與波前垂直)
sinθ1 = λ1 / hc
sinθ2 = λ2 / hc
兩式相除並以速率代換替波長
sinθ1 / sinθ2 = λ1 / λ2 = v1 / v2
現在我們可以由光速在真空與介質中的不同來定義該介質的折射率:
n = c / v
其中 v 是介質中的光速。
對於兩種介質,n1 = c / v1、 n2 = c / v2,由前面的結果
sinθ1 / sinθ2 = v1 / v2 = n1/ n2
即 (司涅耳)折射定律
n1sinθ1 = n2 sinθ2
得證。
如何在馬克斯威爾方程式中看到惠更斯原理?
波長與折射率
現在之看光線從一個介質進入另一個,伴隨光速之改變所造成的波長變化情形。因為光速與介質有關,因此波定與介質有關。假設某單色光在真空中有波長 λ 與光速 c, 在介質中則有波長 λn 與光速 v,該介質折射率是 n,則前面根據惠更斯原理 得到的 v1 / v2 = λ1 / λ2,我們有
λn = λ v / c
其中將折射率 n = c / v 用上,則
λn = λ / n
這說明了同一道光,在介質中的速度不一樣、波長就不一樣。
至於頻率,則是相同(見課本),這是深植在惠更斯原理中。
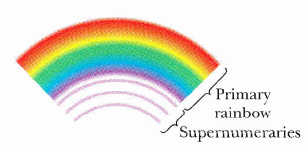
彩虹與干涉
繞射
"要準備干涉現象,要先了解波之繞射的基本特性"(why ?)
"為了準備干涉現象的討論,要先介紹波之繞射的觀念",後面會再談到更多。見水波實驗圖,以及入射波圖解,孔洞若夠小與波長相近,通過之波會向外散開,這就叫繞射。
楊氏干涉實驗
第一個證明光是波的實驗
這個實驗讓我們看到亮暗紋
條紋的位置
ΔL = d sinθ
圖 35-7
d sinθ= m λ (亮紋)
d sinθ= (m + 1/2) λ (暗帶)
同調性
要看到干涉條紋,則到達幕上任一點的光波都要有 "不隨時間變化的相位差"。楊氏干涉實驗中 S1 與 S2 出來的光 "完全同調" ,它們來自通過 S0 的單一個波。
陽光是部分同調,是說陽光只有在截面上靠近的兩個點才有固定的相位差。
讓光通過狹縫,才能產生同調光,並且由於狹縫小,也才均勻繞射到兩個狹縫上,而利於干涉實驗。
若用兩個獨立光源,如兩白熱燈,則沒有同調性(課文說相位的變化快到眼睛看不出來干涉)。
雙狹縫干涉的強度
前面的 d sinθ= m λ或 (m + 1/2) λ 給的是極大與極小的位置,在此則要給出強度隨角度的分佈:
I = 4 I0 cos2(φ/2)
其中
φ= 2πd/λ sinθ
由這兩式,分析最大亮度與最小亮度要發生在什麼位置角度,則可得回 d sinθ 公式。
上兩式 35-22, 35-23 之證明
利用 phasor 方法處理
E1 = E0 sin(ωt)
E2 = E0 sin(ωt + φ)
phasor 合成
E = 2 ( E0 cos β )
其中 β= φ /2 (等腰三角形兩內角和等於第三角之外角)
I ∝E2 = 4 E02 cos2 φ /2
I / I0 =E2 / E02
I = 4 I0 cos2 φ /2
得證
圖 35-7b
相位差 = (2 π/λ) 路徑差
故
φ= (2π/λ) ΔL = 2πd/λ sinθ
得證
兩個以上的波合成
(1) 畫出一組相量(phasor)來代表代加函數,將這些相量保持相位關係頭尾相接
(2) 用一向量連起上述相量和的尾到頭。此向量和的長度為合成之振幅,與第一相量之夾角為與第一相量之相位差。向量在縱軸上的投影則是合成波對時間的變化。
例題 35-4
薄膜干涉
考慮幾乎垂直、厚度很小
反射之相位偏移
case 1 粗繩 到 細繩
case 2 細繩 到 粗繩
重球 撞 輕球 v.s. 輕球 撞 重球
薄膜干涉方程式

薄膜厚度遠小於 λ
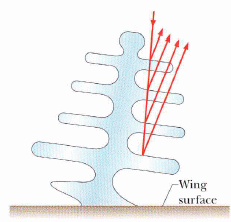
蝶翼與紙鈔的變色現象

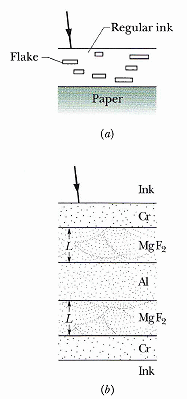
邁可森干涉儀
距離 (的變化) 可以用光波作精確的測量
1/4 λ的長度變化,就可以條紋由亮轉暗。
(以太不存在,史上 "最成功的失敗實驗")
繞射現象
繞射與光的波動理論
前章在介紹楊氏雙狹縫干涉的時候有提到,單狹縫拿來作為獲得完全同調光源的光。波長與狹縫相當的光波,在通過狹縫後,以球形波方式散開,主要還只在討論光線離開狹縫沒多久後的波前概況。
本章要比較完整地探討,討論繞射波在傳播比較遠之後,因波動性質所能造成的強度變化及其不同的應用面相。
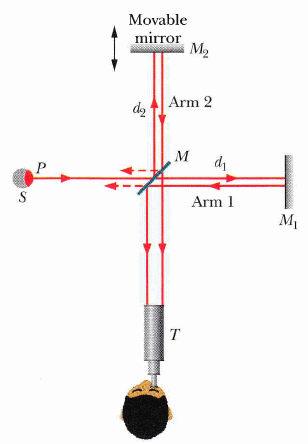
弗瑞奈亮點
法國科學院內光粒子派支持者的積極辦活動,與繞射有關的論文的有獎徵文。
帕松提出,如果弗瑞奈之論正確,將會有光像進入球體陰影而在中心有一亮點的 "奇異結果",
單狹縫繞射:找出極小的位置
利用簡單而巧妙的方法,把整個單狹縫看成偶數個組的等寬通道,如圖。對於遠處屏幕的一點,如果相鄰通道的第一道光路徑直線成對造成破壞性干涉,則可想像平移任一小段的成對光路徑全部都抵消,故為一暗點。
a / 2 sinθ = λ/ 2
即,
a sinθ = λ
以上是第一極小(暗紋)出現的角度
同理,第二極小可分成四段,
a / 4 sinθ = λ/ 2
即,
a sinθ = 2λ
以上是第二極小(暗紋)出現的角度
以此類推
a sinθ = m λ
m = 1, 2, 3 . . .
(為什麼不能用奇數分段?因為會配不完,一定要偶數段。)
單狹縫繞射強度的定性分析
相位差 = (2 π / λ) 光程差
Δφ = (2 π / λ) sinθ
再利用 phasor 方法相加
幾種可能的情況如圖 36-6
單狹縫繞射強度的定量分析
強度(亮度)與角度的關係是
I(θ) = Im ( sinα/α)2
其中
α = 1/2 φ = (πa / λ ) sinθ
依強度公式去分析,的確會導致有暗紋發生在
a sinθ = m λ,m = 1, 2, 3 . . .
上兩式(36-5 式 及 36--6 式)之證明
以 Δx 作必微分段,用 phasor 方法累加各光束不同相位差之貢獻。
見圖 36-8
相位差 phi 在此幾何中有以下關係
sin (φ/2 ) = Eθ /2R
將圖中 Em 考慮成弧形,可以將弧度表示成
φ = Em / R
將 R 代入上上式,則有
sin (φ/2 ) = Eθ / 2R = Eθ φ / 2 Em
因為強度與電場平方呈正比
I(θ) / Im = Eθ2 / Em2 = [ sin (φ/2 ) / (φ/ 2 ) ]2
故
I(θ) = Im [ sin (φ/2 ) / (φ/ 2 ) ]2 = Im ( sinα / α )2
得證。
再來,要找 α 與 θ 之間的關係,利用相位差與光程差之間的關係
φ = (2 π / λ) a sinθ
故
α = φ/2 = ( πa / λ) sinθ
得證。
圓孔繞射
sinθ = 1.22 λ / d
回憶單狹縫繞射的第一極小位置
sinθ = λ / d
有類似之處,其中 1.22 是圓孔形狀所造成的。
鑑別率
透鏡成像是繞射圖樣的事實,促使我們必須研究物與像對應的問題,也就是鑑別率問題。
鑑別率與角度的關係
兩點光源的繞射結果,如果接近到其中一個的中央極大落在另一個的第一極小上,則認定為開始不能分辨,
θR = sin-1(1.22λ/ d)
小角度時,為 sinθ 與 角度 θ 可近似為一樣
θR = 1.22λ/ d
請注意前兩式得到的θR 並不是兩物體間距造成的角度。實際觀察時的視角 θ 還要跟 θR 來比。
這裏的 d 是光學系統中(最小)的孔徑大小
這個視角度,來自 D / L 的分析,其中
利用透鏡來鑑別小角度間隔之物體,必須使繞射效應儘量減小。由本節本討論,增加透鏡直徑或減小波長皆可達到此目的。(相機越好、鏡頭越大;藍光 DVD 記錄密度比過去的紅光高。)
雙狹縫繞射
前章有講過雙狹縫干涉,這裏更進一步談雙狹縫繞射。
見圖
相當於是一個單狹縫繞射與一個雙狹縫干涉乘在一起,
I(θ) = Im (cos2β) (sinα / α)2
其中
β= ( πd / λ) sinθ
α = ( πa / λ) sinθ
(無限遠光源繞射是相當於富利葉轉換,長物件得短條紋;短物件得長條紋。)
繞射光柵
亮線發生在,見圖
d sinθ = m λ
m = 1, 2, 3, . . .
線寬
第一極小在
N d cosΔθhw = λ
中央線半寬度
Δθhw = λ/ N d
(不證明,直接給)
在θ 處之線的半寬度
Δθhw = λ / ( N d cosθ )
光柵分光儀

光學可變圖
全像片曾作拿防偽,但效果不好。(1) 近看才清楚,(2) 易仿(實物拍照)
很多卡改用 OVG,每個部分都有不同的光柵,看得清楚,又很難反推去決定光柵條紋的細節。

光柵:色散與猛鑑別度
色散度
D : = Δθ / Δ λ
D = m / (d cosθ )
鑑別率
R : = λavg / Δ λ
R = N m
36-30 式的證明
36-32 式的證明
色散度與鑑別率的比較
組織化層狀結構的繞射
X-射線繞射
1912 年德國科學家 Max von Laue 想到,晶體裹的原子也可以扮演繞射光柵的角色,來對 X-射線產生繞射。
會產生建設性干涉的分析,見圖:
(在作圖上雖然以有原子構成的虛擬平面來作為反射 X-射線,像是處理薄膜干涉的那樣,但結果是仍是對的)
這個虛擬的平面,只有某些地方有原子,這個跟在不同面上隨便取一些原子拿出來做繞射的探討(則結果一定會不同),有什麼不一樣?在我們定出的面,雖然不是面的處處都有原子,則另一個面也沒有在正下方有原子,但是有很重要的一點,就是面上的原子排列有規律性、週期性,並且定出來的面之間也有會重覆的週期性。
2 d sinθ = m λ
其中 m = 1, 2, ....
這裏的分析處理方式,稱為 kinematics 理論,這是一種工具性的理論,以比較簡化的近似方法討論。另有 dynamics 理論,有較完整的理論推導。一個比較完整的的計算方法,是把整個晶體作富利葉轉換,而由於富利葉轉換是線性的,因此一層一層可以拆開來處理,至於對單一層的散射,則依惠更斯原理的探討,反射角等於入射角。
獲得可以了解原子如何在晶體中排列的工具,不但開啟了固態與材料物理的研究,也促成了 DNA 密碼的解出,對於物質科技與生命科技的發展有關鍵性的貢獻。
繞射引發的結構性顯色
見圖 36-28
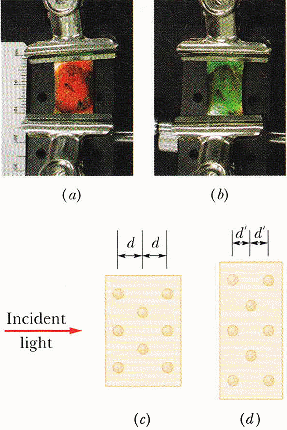
例題
36-3
36-4