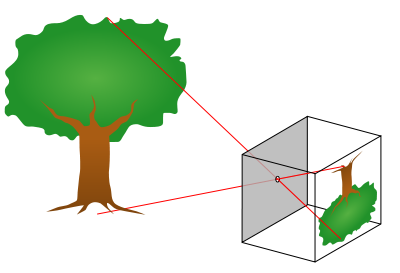
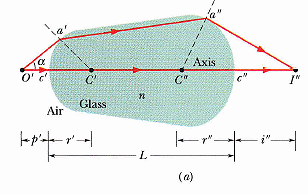
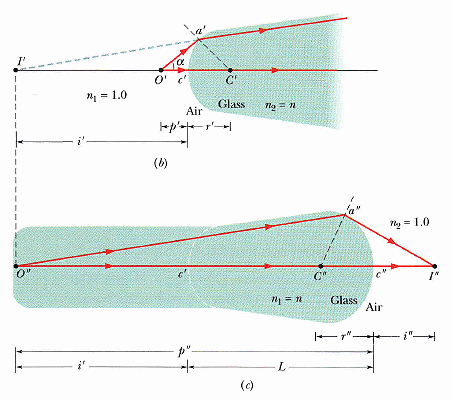
要能看得見形體,最基本要求就是物體表面的一個點必有,且只能,映射到一個點,相鄰的點會映射在相鄰的區域。(正確的比例只並不重要,大腦會自行修正或忽視,或僅取用需要的資訊而不會感到奇怪。)
視線(或光跡)
視覺糸統藉由收到的影像,帶來意識,我們可以感知物體所在的方向與遠近。
簡單地說,物體位於視線延伸的方位。墨經中也提到,目視可以用來描準射箭。
兩種成像
實像 (Real Image)
物體的確位於視線延伸的方向上。
實像可以成像在一個平面上。
虛像 (Virtual Image)
物體並不位於視線延伸的方向上。例如光線是經過反射才到達眼晴。
常見的海市蜃樓 (Mirage)
空氣密度不均造或之光路徑的彎折。見圖
平面鏡 (Plane Mirrors)
一個物體置於平面鏡前,投射在該物體上的光以不同方向投射到平面鏡的不同位置上,如圖 34-2。
利用反射定律,物體的光透過鏡面反射進入眼中,造成其視線方向的延伸有一個虛像(鏡像)的感覺。如圖 34-4 。習慣上取物距 p 為正值,所以在此的像距(虛像)是負的。
i = -p
有長度的 (延伸的) 物體
虛像 I 和物體 O 有一樣的方向與高度。
鏡子迷宮
見圖 34-7,(a) 實體,(b) 鏡像;(c) 包合自己的反射路徑,(d) 看到自己們虛像。(課本暗示尚有一個看見自已的方向,問要朝那裏看才看得到?其實 (c) 的光線路徑還存在一條是逆走的。)
球面鏡
若鏡面彎曲,則像如何變?考慮球面鏡,其鏡面為球面的一部分。
看到的鏡像,向我們凹的會放大,向我們凸的會縮小。凸面鏡像距變近,可視範圍變大,常見於轉彎處或超市監視用。
球面鏡的焦點
平面鏡的像距 i 等於物距 p,但球面鏡不同。考慮平行光入射凹面鏡,反射光通過一點 F。若在 F 上放一張卡片,則無限遠處物體 O 的影像會顯現在卡片上面。若是凸面鏡,則沒有實焦點而只有視覺上的虛焦點。
凹面鏡的實焦點 F 其到鏡面中心 c 的距離被定為正的焦距 f,凸面鏡者則是負的。如此定則它們與曲率半徑 r 有以下關係:
f = r / 2
見圖 34-10 (a),物體 O 放在焦點內,形成虛像,方向與物體相同
見圖 34-10 (a),物體 O 放在焦點上,實、虛像皆不成像(來自 O 點的光不交會)
見圖 34-10 (b),物體 O 放在焦點外,形成實像(從無限遠處移入),方向倒立。
在球面鏡的例子中,實像的像距是正數,虛像則是負數。我們總是會看到:"球面鏡的實像與物體同側,而虛像則在另一邊。"
如果來自物體的光線僅與中射軸夾小角度,可證明
1/p + 1/i = 1/f
(即:1/物距 + 1/像距 = 1/焦距 )
物高 h、像高 h' (從中心軸量起),橫向放大率 (Lateral Magnification) m 可定義為,其大小是像高與物高的比例
| m | = h'/h
其正負號則顯示像的方向是與物體相同 (+) 或相反 (-) 。
球面鏡的橫向放大率可被證明為是
m = -i / p
自行填入面鏡表是整理及預測光學成像的一個有利工具,請看 表 34-1。
畫光線以決定像位置
圖 34-11 (a), (b) 所示為凹面鏡的情況,下列四條射線取兩條可協助我們定出像的位置:
(1) 平行於軸之光線,反射穿過焦點(這點前面有說明過)
(2) 穿過焦點光線,反射後 平行於軸
(3) 穿過曲率中心之光線,反射後 原路徑返回(球面性質)
(4) 射到鏡面中心 c ,反射你線對稱於中心軸(反射定律)
找出物體上兩個或兩個以上的點,各點作上述畫線(四選二)求交點定其各點像的位置,即可討論成像。
圖 34-11 (c), (d) 所示為凸面鏡的情況,上述作圖規律僅需稍作修正(見圖 (c), (d) 並注意文字說明),即可使用。
m = -i / p 的證明
考慮圖 34-11 (b) 的射線 4,abc 與 dce 為相似三角形(角度全同),故
de / ab = cd / ca
上式右手邊是像高、物高比,故為橫向放大率 m 的絕對值 | m |。此像為倒立,之上式等號左邊為 -m。另外再看, 等號右邊,cd = i、ac = p,故
m = -i / p
得證。
按平行光透過後的行為,分為 會聚透鏡 (Convergent Lenses) 與 發散透鏡 (Divergent Lenses) 兩種。
(直接先介紹公式)"薄"透鏡是指厚度比 p, i , 兩面的曲率半徑 r1, r2 小很多。我們若只考慮小角度(光線與中心軸),則可證明薄透鏡有焦點在焦距 f,且滿足
1/f = 1/p + 1/i
又有 "造鏡者方程式"(折射率 n 的薄透鏡用於空氣中),
1/f = (n -1) (1/r1 - 1/r2)
r1 為靠近物體之透鏡表面的曲率半徑, r2 為另一面的。
透鏡能彎折光線故能將物體成像,而其能彎折光線是因為折射率與周圍環境不同,見圖 34-15(至於為何彎折,也可由光的波動行為理解,見下一章)。故空氣中用的眼鏡在水中度數不準。
會聚透鏡實焦點,故應令 f 為正(這與凹面鏡作法相同),由造鏡者公式中去檢驗:n - 1 > 0 ,且 r1 > 0 (與光源同側), r2 < 0 ,故的確 f > 0。
薄透鏡成像
圖 34-16
如同面鏡的作法,當有實像時像距 i 令為正,虛像的像距令為負。
實像與物體在透鏡的不同側,虛像與物體在同側。
畫線找出有長度物體之像距
圖 34-17(利用三條特殊的光線)
(1) 平行中央軸射線,透射後穿過遠側(另一側)焦點 F2 (// -> F2 )
(2) 通過近側(同側)焦點 F1 之光像,透射後平行中央軸 (F1 -> //)
(3) 指向透鏡中心的射線,透射後方向不變(因穿透處兩側近乎平行)(pin-hole at center) 或(straight through center)
雙透鏡系統
假設近物體透鏡 1、遠的為 2,兩步驟:
(1) Find i1 from p1 and f1
(2) Remove L1, use i1 as p2 to find i2 using f2
M = m1 m2
例題 34-5
簡易放大鏡
我們要把東面看清楚而把東西移近,但太近卻比眼睛所能見的距離(近點 (Near Point,Pn,如圖 34-19)更近。

看放大鏡如何改善此一情況。
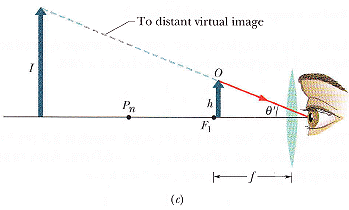
凸透鏡的存在使物體己在近點之內還能看清楚。
以下估計放大倍率:
mθ = θ' / θ
for small angle, θ ≈ tanθ , then
θ ≈ h / 25cm, θ' ≈ h / f
we have
mθ≈ 25 cm / f
註:其實本節的討論同時包括老花眼鏡及放大鏡,你能分得出來各自的部分嗎?
複合顯微鏡
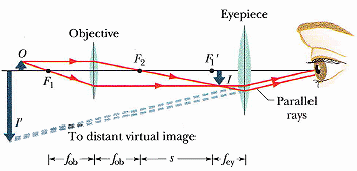
被觀察物體放在物鏡的 F1 外,且極接近 F1 ,故 p ≈ fob
接著,調整兩透鏡距離使物鏡的放大倒立實像(為什麼是放大?想想)I 的位置正好落在目鏡的第一焦點 F1' 內。(落在焦距內,所有會有虛像,而離焦距近,故像會放大很多,見前薄透鏡之作圖)
現在探討物鏡放大率,需 i 及 p, 前己有 p ≈ fob
管長 s >> fob
i ≈ s
故
m = -i / p = s / fob
再看目鏡,因 I 落在目鏡的第一焦點 F1' 之內,即相當於簡單放大鏡
再套用放大鏡放大率公式 mθ,則總和放大率
M = m mθ = - ( s / fob ) (25cm / fey )
折射式望遠鏡
考慮兩片透鏡式的簡單望遠鏡(實際上,物、目鏡之常都各是複合透鏡系統)。
望遠鏡與顯微鏡之鏡片排列方式看似相似,功能不同,前者用來看很遠的物體,而後者卻相反。注意 圖 34-21 中物鏡的第二焦點 F2 與目鏡第一焦點 F1' 重疊,而顯微鏡 圖 34-20 中兩者分隔了管長 s 的距離。
策略如下:物體在非常遠故發自其某一點的各光線進入物鏡時近乎平行(但物體總有大小,這些光以角度θob 平行進入)。因平行故以像高 h' 成像在 F2,而這裏恰是目鏡的 F'1 故它通過目鏡後是平行光,進入眼睛的角度是 θey,只要 θey > θob 就是有(對非常遠處的物體)放大的效果。
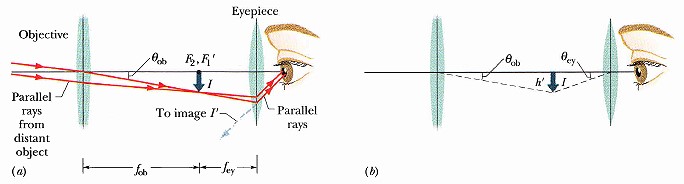
望遠鏡的放大率是有使用與沒使用望遠鏡看到物體佔據的角度的比值:
mθ= θey / θob
對靠近光軸的光線,θob ≈ h' / fob 、θey ≈ h' / fey(物鏡像高 h' 在這裏變物高,而此處是物鏡第一焦點意味著通目鏡後來自 h' 點的光線將會平行,則通過透鏡中心 c 的光線有代表性可代表其他與之平行的光線與中心軸的夾角,故此θey ≈ h' / fe),代入上式得
mθ = - fob / fey
其中負號表示是虛像。
由上式我們可以體會,望遠鏡倍率要大就要有一長一短焦距的組合,且總長度是兩者之和,這也是為什麼傳統望遠鏡總是長長一支,且倍率越大越長。
放大率容易達成,而亮度(與透鏡面積有關)、鑑別率與視野均是重要且有高難度的因素。
另有球面像差及色像差的問題。