�Q�ΤU���� 32-11�A�Q�����w�߳y�����ϰ����x
�ߧ��Ʋ��ͤϦV���ϯx�A�Y�Ӻϳ��D���áA�h�Ϻϧ��ƨ����O�A�N�Ϻϧ��Ʊq�ϳ��j�B���ܮz�B�C
�a�B��ϳ������C��A���� 32-12
�ϲ~�����b���o�����
���J���º���{���B���誺�ϩʡB�q�Ϫi
���J���º���{��
�ϳ��������w��
�ϳ淥�]�ثe�Ҫ��^�ä��s�b
ΦB = ∫CS B · dA = 0
����q���������w��
ΦE = ∫CS E · dA = qenc / ε0
�ϧ馨�X�q�A�C�@�q���ܦ����K�A�U�ۦ� N�BS ���A�p�� 32-2
�Q���D�G�ҥH�A���_�����K�A�����ۤw�i�H�l�b�@�_�O����Ӫ��Ϊ��A��ܡH
�P�����ͪ��ϳ� (Induced Magnetic Fields)
�k�ԲķP���w�߬O "���ܥq"
∫CL E · ds = - dΦB / dt
�Ӱ��J���º��P���w�߫h�O "�q�ܥͺ�"
∫CL B· ds = μ0ε0 dΦE / dt
�����ҩ����T�p���C
�o�طP�����@�ӯS���Ҥl�O���b�R�q�����q�e��
�w���а��J���º��w��
�^�Цw���w��
∫CL B · ds = μ0 ienc
�ӫe�@�p�`�����J���º��P���w�ߵ�������A�]�X�{�P�˪��ϳ������n���A�ڭ̥i�H�X�ֳo��Ӥ�{���G
∫CL B · ds = μ0ε0 dΦE / dt + μ0 ienc
�٬� �w���а��J���º��w��
�첾�q�y
�o�O���J���º��̫�ΦX�|���@�դ�{�����̫�@�����ϡ]�F�����������R�P����^�C�ڭ̬ݤW���� �w���а��J���º��w�ߤ������k�䪺�ⶵ�A�ӳ]�Q�@���Q�q�y�A�첾�q�y
id = - ε0 dΦE / dt
�h
∫CL B · ds = μ0 id,enc + μ0 ienc
�p���A�N���i�ιq�y���Ӳz�Ѻ������C
�첾�q�y�����z�N�q
�ܰʤ����q���A�i�����q�e�W���R�q�q�����b�ܤƼƶq�]�]���q�O�u���ƥؤ]�~�|�ܤơ^�A�ӯ�y���q�e�R�q���A���O�q�y�C���q�y���O�u���q���ǿ�L�h�A�ӬO�ֿn�b�q�e���W���q�������A�]���~�s�q�첾�C�G�y�������q�e���R�q���R�q���������Q�q�y�A�s�첾�q�y�C
�D�P���ϳ�
��b�| R�A���b�R�q�����O�q�e�A�ڭ̥i�� id �ӨD�P���ϳ����j�p�A�q�e�����Z���߬� r ���I��ϳ��j�p���A
B = (μ0 id / 2πR2) r
�b�q�e���~�h�O
B = μ0 id / 2πr
���J���º���{���]�ա^
�b�S�����q��κϩʽ�s�b�����p�U�A�|����{����z�p �� 32-1 �G
�����w��
�Ͼǰ����w��
�k�ԲķP���w��
�w���а��J���º��w��
���J���º���{���]�ա^�]���L������
�o�|�Ӥ@�ժ���{���y�z�Ҧ����[���ϡB�q�B���{�H�A�Ʀܥ����t�פ]�æb�䤤�C�T�w�����t���٤o�F��N���z���s���R�C
���誺�ϩ�
���K
�a�Ϫ��o�͡A�q�ʾ���z
http://en.wikipedia.org/wiki/Dynamo_theory
��s���v�s��ⰼ���O���]���ϡ^�A���C�ʸU�~����
http://www.sciscape.org/news_detail.php?news_id=1477
�ϩʻP�q�l
�۱ۺϰ���
μs = − e/m S
S ���P�j��O�Ǥ������ʶq�A������ӭn�I�G
(1) S �����L�k���q�A�ϦӬO�u���@�b�����q�i�H�Q���q
(2) S ���i���q���q�O�q�l�ƪ�
Sz = ms h/2π�A�䤤 ms = ± 1/2 �]h/2π=
h�A�G Sz = msh�^���q�l�m��~�[�ϳ� Bext ���A
U = −μs· Bext = − μs,z Bext �]�䤤 z �� Bext ����V�^
��q�l�Q�������y���ҫ��Ӳz�� "�۱�"�]���ƹ�W�ä�����^�A���� 32-9
��l�P���l�]�U���䨤�ʶq�κϯx�A���l�Ө�����̦P�V�A�襤�l�Ө�����̤ϦV�A�o�ǰ����x���l�ϳ����^�m��q�l���p�@�d���C
�y��ϰ���
μorb = − e/2m Lorb
Lorb ����Q���q�A�u���u���N��V�����q�A�p Lorb,z�A�i�H
Lorb,z = ml
h�Aml = 0, ±1, ±2, ±3, ... , ± maxU = −μorb· Bext = − μorb,z Bext �]�䤤 z �� Bext ����V�^
�q�l�y�D���j���ҫ�
���]�q�l�H�j���l�b�|�ܦh���Z��¶��l�@��P�B��
μorb = i A
�յ۩w i
�q�� e�B�g�� T = 2 π r / v
i = e / T = e v / 2 π r
�N�j�����n A = π r2 �s�P i �@�_�N�J�A��
μorb = i A = e v r / 2
�Ө��ʶq l = m (r × v)
Lorb = m r v sin 90° = m r v
μorb = − e/2m Lorb
μorb = − e/2m Lorb
�o���ŦX�e���y��ϯx�����G�C
�Ъ`�N�������A�Ω�b��l�����q�l�A�]�P��L�z�פι��礣�ŦX�C
�D���ó������j���ҫ�
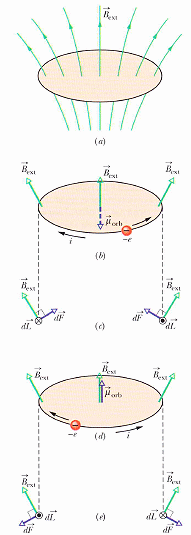
���� 32-11�A�ϰ����x������ϤO�C
dF = i L × Bext
�ϩʧ���
�Ϻϩ�
�j���������ݤ��C�b�~�[�����Q�o��ܡ]�ƥ��^�~�[�����z�ϯx�C
���ϩ�
�L��A�}�g�����A��l�W���W�ߪ��ϯx�C
�K�ϩ�
��l�W���ϯx�洫���X�ӱƦC�_�ӡC
�Ϻϩ�
�Q�ΤU���� 32-11�A�Q�����w�߳y�����ϰ����x
�ߧ��Ʋ��ͤϦV���ϯx�A�Y�Ӻϳ��D���áA�h�Ϻϧ��ƨ����O�A�N�Ϻϧ��Ʊq�ϳ��j�B���ܮz�B�C
�a�B��ϳ������C��A���� 32-12
�ϲ~�����b���o�����
���ϩ�
�b�~�[�ϳ��v�T�U�A��l�ϱ��ͦV�V����ƦC�Ӧ��b�ϯx�C���ϯx�åB�Q�Q�ϳ��l�ޡC
�ϤƱj�� M = ���o���ϯx / ��n
M = C Bext / T
���ϡA�ȾA��p Bext / T ��
�K�ϩ�
�ϰ�]�ϰϡ^
�ǥѩҿת� "�洫���X" (exchange coupling)�A�F���l�W���ϯx�|�ƦC�_�ӡA�Φ��j�j���ϳ��]�ϯx�^�C �s�۵o�ʺϤ�
�Y�ϭ�l�ƨ������洹�κA�A�]�����P�ϰ�A��l�ϯx�u�b�ϰ줤�ƦC����A���P�ϰ�}�ϯx��V���P�ө���C
�Y�W�L���ƪ��~§�ūסA�h���A���۵o�ϤƲ{�H�Ӻϰ줤���ϯx���A����ƦC�A�ɭP�ϩʮ����C�]�j�P�q��N�n���۰ʸ��O�ŴN�O�Q�κ��K���~�z�ūסC�^
���e�O���ۦa�y�ϳ�
�����C�ƨ��K�q�@�L���ɧY�O��@�ϰ�A�G���S�w�����x�C�@�e��踮Ƨd�a�B�G�κA�A�ϯx���a�ϼv�T���V�n�_�A�����V�T�w�C�Q�Φ~�N�[�������e�i���R�X���ɦa�Ϥ����C
�Ϻ�
�Ϻ����u�A����
"�O��" �@��
"�O��" �@�ι�O���C��]�p�ϺФ��^�ܭ��n�C�]�_�h�N�O���F��T�F�^
�q�Ϫi
���J���º����m�i
���J���º������j���N�O�ҩ��F���N�O�q���P�ϳ��ҧΦ����q�Ϫi�C
��i�q�Ϫi�����w�ʤ��R
���ͦ�i�q�Ϫi���˸m
���� 33-3�A�@�� RLC �q���ðt�X�ѽu�A�N����o�g�q�Ϫi�C
��i�q�Ϫi�����n�S�x
1. E�BB �U�۫������i��V
2. E�BB ���۫���
3. E × B �Y�O�i��i����V
4. ���`�O�̥��������b����
E = Em sin(kx - ωt)
B = Bm sin(kx - ωt)
�i�t
c = 1 / √(μ0ε0)
E / B = c
�@�ӳ����H�z�Ѫ��i
�q�Ϫi�èS���]���ݭn�^�Ǽ����C���A���t�b�Ҧ��y�Шt�������@�˪��ȡC���P�ɶ��@�_�A�O�ɪŶ����c���@�����C
��i�q�Ϫi�����w�q���R
�q���P�ϳ��������P���i���ѧڭ̥��C
���� Em / Bm = c
�b dx ���Z������ݡA�q���� E �P E + dE�A�� h �@���ӻP dx ���e�Φ������n�ءA�Q�ӭ��n�j�������P���ϳ��A�Q�Ϊk�Բĩw��
∫CL E · ds = − dΦB / dt
∫CL E · ds = ( E + dE ) h - E h = h dE
ΦB = ( B ) ( h dx )�A�G
dΦB / dt = h dx dB/dt
�N�J�k�Բĩw�ߡA�o
h dE = - h dx dB/dt
�Y dE / dx = -dB / dt
�ƹ�W�AE�BB �Ҭ��ɶ��P�Ŷ�����ơA�W�����@
∂E / ∂x = -∂B / ∂t
�ڭ̧� E = Em sin(kx - ωt) �� B = Bm sin(kx - ωt) ���@�O�v���A�h��
∂E / ∂x = k Em cos(kx - ωt)
∂B / ∂t = - ωBm cos(kx - ωt)
�G��
k Em cos(kx - ωt) = ωBm cos(kx - ωt)
k Em = ωBm
�ڭ̪��D��i�i���i�t�]�۳t�ס^�O ω/ k �A�G
Em / Bm = ω/ k = c
���� c = 1 / √(μ0ε0)
���Ҥ�
�� 33-7
�Q�� dx �d��ⰼ���ϳ��� B �P B + dB�A�Q�κϳ������n���P�q�q�q�ܤ����Y�� �w���а��J���º��P���w��
∫CL B · ds = ε0 μ0 dΦE / dt
∫CL B · ds = - (B + dB) h + B h = -h dB
�Ъ`�N�ѩ�j����V���]�w�A�W�����Ĥ@���O�t��
ΦE = ( E ) (h dx)
��W���L��
dΦE / dt = h dx (dE / dt)
�t�~�`�N �W����ɶ��L�����|�@�Ψ� dx�A�]���o�ر��Q����ƬO���A����Ө� x �u�O�Ŷ����R�x���ܼơA�����O�ɤl���y���� x(t) ���ˡC
�����N�J�w���а��J���º��w�ߡA�o
-h dB = ε0 μ0 h dx (dE / dt)
-∂B / ∂x = ε0 μ0 ∂E / ∂t
�{�b�N�J B�BE ����i�i���������
- k Bm cos(kx - ωt) = -ε0 μ0 ωEm cos(kx - ωt)
k Bm = ε0 μ0 ωEm
Em / Bm = 1/ ( ε0 μ0 (ω/k) ) = (1/ ε0μ0 ) (1/ ( ω/ k ) ) = 1/ ε0μ0 c
�ѫe���v���� Em / Bm = c�A�h�o
c = 1 / √ ε0μ0
�]�q�o�اA�i�H�ݨ�A���t�N�æb���J���º���{�����ءC���t�����q�A�i�H���O���q�e�ιq�P����Ӷq��C�^
��q�ǿ�P�i�L�F�V�q
S = 1 / μ0 E × B
S = 1 / μ0 E B
�]�� E / B = c
S = 1/(cμ0) E2
�H�W�O��������q�y�v
I = Savg = 1/(cμ0) [ E2 ]avg = 1/(cμ0) [ Em2 sin2(kx - ωt) ]avg
Erms = Em / √2
I = 1/(cμ0) Erms2
�ݡA�o�ح��q�����j�����ܡH
�ѹq������q�K�ץX�o�i�}
uE = 1/2 ε0 E2 = 1/2 ε0 (cB)2 = 1/2 ε0 c2 B2 = 1/(2μ0) B2 = uB
��n����ϳ���q�K�C�]���A�o�ح����q����q�K�P�ϳ���q�K�O�@�ˤj���C
�j���H�۶Z���ӧ���
�@�ӯu�ꪺ�q�ϴT�g���A��j���H�Z�����ܤƬO������
����q�u���A�Ҽ{���I����
�j�� = �\�v / ���n = Ps / 4 π r2
�����T�g��
����������q�A�]���ʶq�C
�����l���ҳy�����ʶq����
Δp = ΔU / c
�u����|�ҳy�����ʶq����
Δp = 2 ΔU / c
�Y�O�����l�������Ϯg�A�h�ʶq���ܤ���W��̤����C
�Ѥ��y�w�ߡA�ʶq�ܤƻP�O���������Y��
F = Δp / Δt
�t�~�A�����y��n�H�T�g�j�� I �Ӫ��ܴT�g���A�Ъ`�N�j�O
�j�� = �\�v�����n = �]��q���ɶ��^�����n
�G��
ΔU = I A Δt
�h�A�粒���l��
F = Δp / Δt = ΔU / ( c Δt ) = I A Δt / ( c Δt ) = I A / c
�粒���Ϯg
F = Δp / Δt = 2 ΔU / ( c Δt ) = 2 I A Δt / ( c Δt ) = 2 I A / c
�h�T�g���A�粒���l����
pr = I / c
�粒���Ϯg
pr = 2 I / c
�T�g������ Radiometer
����
�q���O�b�@�ӥ����W�����A���� 33-9
������
�q���O�o�X���q�Ϫi���S�w������V�A�@������Τ���h�O�H�������A�]�s�D����
�i�ǥѳq�L�������ӧ�D�������ܦ������Χ����������A���]�������W���ƦC��z�p�p����������l�C
��z�����������j��
I = I0 / 2
��v���������Ө��A�Y θ ���P���������\�q���q�L��V������
Ey = E cosθ
I = I0 cos2θ
�� ���D 33-2 ����
���������ͬ�����
3D �q�v
�����B�}���ΤӶ�����
�z�L�w�C����������Ӭݮѥ��L��o���ҵo�X�Ӫ������]�ЫDz{���ۻs�v���A�I���U�ϧY�i����^
�ۥ��ʻP�}���˴�
�}���l���۩ʡ]�p���k�⦳�蹳�ʺ١A�����k��o���@�ˡ^
�����ɥR�G�Ϯg�P��g����z
�O�ǬO���z�Ǫ��֤߲z�סA���z���w�ߴy�z���z�q���������Y�A�ӤO�ǫh�չϨt�ΤƦa�إߦu���q�P�u���ߡ]��٩ʡ^�C�O�Ǫ������n��`�ơ]�u���q�^�A�p��q�A�������~�A�O�Ǥ]�إߤ@�Ƕq�]�Ҧp�@�ζq�^�A�Ө��Ƕq�����ȷ|���X���z�w�ߡC
�O�����̳t���|��z
�q�@�I��t�@�I�A���� δL = 0 �����|�A�䤤 L �O��g�v���W���|���M�C
���ɧ�g�w��
�ϫݴӤJPauli Lecture of Physics Vol.2 Fig.1.2
L = n1 P1Q + n2 P2Q
L = n1 a1/cosθ1 + n2 a2/cosθ2
�S�A���U����
A1A2 = n1 a1tanθ1 + n2 a2tanθ2 = �`��
�Q�� Lagrange multiplier ��k
δL + λ δ(A1A2) = 0
δ( n1 a1/cosθ1 + n2 a2/cosθ2 ) + λ δ( n1 a1tanθ1 + n2 a2tanθ2) = 0
θ1 �P θ2 ���W�ߪ����ܼơA���ܤ��k�즡��z��
a1 ( n1sinθ1/ cos2θ1 + λ 1/ cos2θ1) δθ1 + a2 ( n2 sinθ2/ cos2θ2 + λ 1/ cos2θ2 ) δθ2 = 0
�h δθ1 �P δθ2 ���Y�ƦU�ۥ������s�A�Y
n1 sinθ1 + λ = 0 �A�B
n2 sinθ2 + λ = 0
�����W�⦡�� λ�A�h
n1 sinθ1 = n2 sinθ2
�o�ҡC
���ɤϮg�w��
���� Fig. 1.3
�Q�λ��U�u�A�]�w P �I���蹳 P* �I�]�����S���v�T���G�A�o�u�O���ڭ̮e���ݹϡ^�A�h�ڭ̰��T���Ψ���M�����j��ĤT��G
P0Q' + Q'P* > P0Q + QP*
������Y�A���Ǹ��|�]���O���p�Ȫ� PQ �A P0Q �A�]�N�O
θ0 = θ
�o�ҡC
�Ϯg
���� 33-15
�Ϯg�w��
θ'1 = θ1
�z�����褤���q�Ϫi�]��g�^
��g�w�ߡ]���I�թw�ߡ^
n1 sinθ1 = n2 sinθ2
�ⴲ
��g�v�P�i������
���� 33-17�B18�B19
�m�i
���� 33-20
���Ϯg
�q�K����첨���誺��g�A���i��o�ܤ@�ӱ��p�A�Y�X�g������ 90 ��
n1 sinθ1 = n2 sin 90°
�p��
����
�ѤϮg���ͤ�����
�g�Ѥ����ά����Ϯg�X�����q�`�O���������Τ������������C��������V�O�����ɭ��C
���|���S��
�J�g�B�Ϯg�B��g�Һc�����������Y
�����A�J�g������Ϯg���A�ӧ�g���h���M���g�v�A�p�G�Ϯg�u�P��g�u���� 90 �סA�h�Ϯg�u�����S���q��������ɭ��������C
�p��z�ѳo�Ӳ{�H�H�ݹϡA������������g�u��q���P�Ϯg�u�O���檺�A�i�H�Q���b�ɭ��W����ɱ��ŦX�s��ʡC
θB + θr = 90°
�ѧ�g�w��
n1 sinθB = n2 sinθr
�N�J��M�� 90° ������
n1 sinθB = n2 sin( 90° - θB ) = n2 cosθB
�Y
θB = tan-1 n2 / n1
�Y�J�g�Ϯg���@���O�Ů�A�h n1 �i���@ 1�A�W���Y���� ���|���S�w��
θB = tan-1 n
���D
33-2
33-5
�곡��g�v�]�l���^