磁力與磁場

磁力與磁場

磁場由何產生

磁單極：尚未發現

用電流產生電磁鐵

磁性物質，如永久磁鐵

 

B 的定義

本來可用磁單極的受力來定，但至今未發現，因之改用移動中的帶電粒子所受的磁力來定磁場

F_B = q v × B

這個公式有個名字，叫勞倫玆力，F = F_E + F_B = q E + q v × B，是電磁場造成的力。

右手定則：伸四指 × 捲收四指 = 姆指方向

 

磁力線（磁場線）

從 N 極到 S 極，見 U 型、C 型、I 型磁鐵的磁力線（磁場線）。

 

交叉場：電子的發現 與電視映象管

E 與 B 互相垂直時我們稱之為交叉場 (Crossed Field)

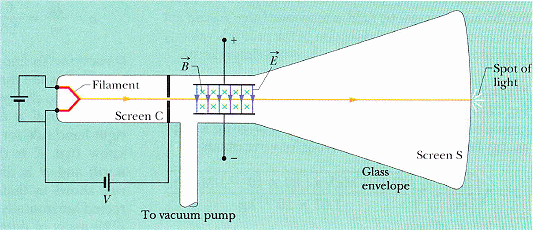
J. J. Thomson 陰極射線管發現電子，1997 (1995?) 電子發現 100 年紀念。

一個現代版的陰極射線管是電視映像管，藉由交叉場 E 與 B

Thomson 大膽聲稱此粒子存在於各種物質，又預測它的質量小於質子的千分之一（事後量得質量比是 1836.15 倍），再加上電荷質量比 m / | q | ，一起被稱為是 "電子的發現"。

 

 

交叉場：霍爾效應

在導線中漂移的電子也一樣會受磁場影響而偏移，事實上這提供了我們可以知道導體內傳送電流的是正電荷或是負電荷。

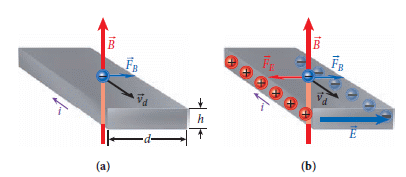
寬度 d、電流 i (漂移速率 v_d)。系統會很快達到平衡，此時橫向寬度建立了一個可量到的電位 V，累積電荷造成的電場 E = V / d 對測試電荷的推力 F = q E 恰等之磁力 F = q v B，故

e E = e v_d B，即 v_d = E / B = V / B d

 

v_d = J / n e = i / n e A

n = i / e A v_d = i B d / e A V = i B / e L V

其中 L 是金屬片長度 L = A / d

n = i B / e L V

上式等號右邊全都只可以測量或設定的量。

霍爾效應也能被用來載子的速率 vd，其大小的數量級大約是每小時幾公分。方法是以機械朝載子傳導的反方向移動整個裝置，直到霍爾電位完全消失，此時表示載子速率 v_d 是零，剛好被平台的移動抵消。

 

讓帶電粒子進行圓周運動

磁力：F_B = q v B

向心力：F = m v² / r

磁力要造成向心力，則 F_B = F，即

| q | v B = m v² / r

可解出路徑 r

r = m v / | q | B

這是等率運動（因為力垂直於行進方向 v × B），其週期 T 則是 周長 2 π r 除以速率 v

T = 2 π r / v = 2 π m / | q | B

則頻率與角頻率各為

f = 1 / T = | q | B / 2 π m

ω = 2 π f = | q| B / m

 

螺旋路徑

只是多加了垂直於面的運動速度，頂出一個維度而成螺旋路徑

 

磁瓶捕捉

不均勻磁場中，如 FIG 28-11 (圖 28-10)

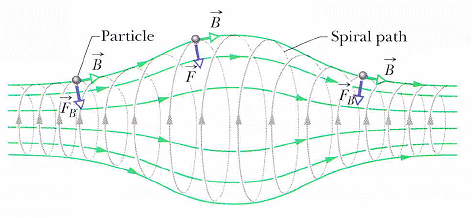
該例中，兩端磁力強，中間弱（因為半徑在中間小，想磁力公式就可以知道）

 

極光

來自太陽風中的帶電粒子，被南北極地球磁場抓住帶入（灌入）大氣層中（地磁強度在兩極最強），而撞擊氣體分子而產生極光。高 100 km、寬 4000 km 的光幕，卻只有 100 m 厚。氧原子發綠光、氮分子發粉紅光，但光色很淡因此極光看起來是白色。

為什麼極光幕很薄？因為旋進極地區密集的磁力線，對電子有會聚的作用。

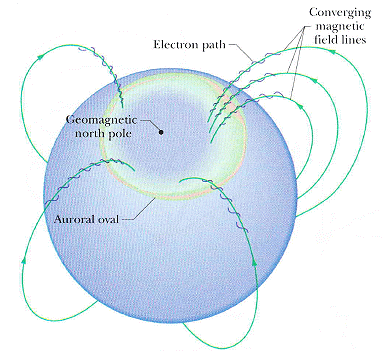
（太陽風、范艾倫帶與地球生命）

迴旋加速器 及同步加速器

迴旋加速器 cyclotron

如何加速帶電粒子？在磁場中之圓周運動的週期是可以知道的（見上）ω = 2 π f = | q| B / m ，它甚至與速率無關。

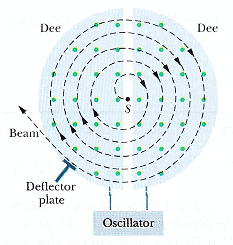
因此可以利用繞圈時的時間點，粒子在左邊時吸到右邊，粒子在右邊時則吸引到左邊，反覆進行達到加速的目的（用一句簡單的話講，就是此一運動有固定的共振頻率，外部施力如果以相同的頻率施加其上 f = f_osc，則會造成共振現象）。此共振的條件為 | q | B = 2 π m f_osc ，對特定粒子而言 q、m 為常數，故調整 B 即可達到共振條件。

 

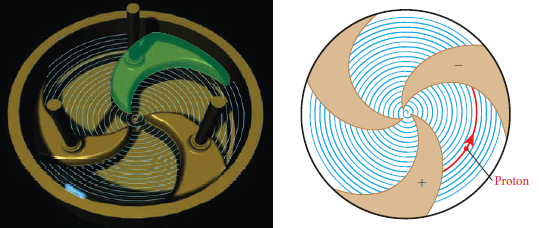
除帶電粒子，中子束也可用 迴旋加速器 獲得，作法是加速 氘核 去撞鈹靶，鈹核內會有中子被撞出來，這些中子被用來破壞特定區域腫瘤細胞的 DNA 。迴旋加速器不是以直線來加速粒子，所以體積較小仍可以在醫院中被使用。

補充：粒子放射冶療

 

質子同步加速器

用上述裝置加速質子僅可達 50 MeV 之動能，原因有二，(1) 相對論效應造成質量增加，(2) 以到達到 500 GeV 為例，在 1.5 T 的磁場下，其圓周半徑己達 1.1 公里，將需要一個 4 × 10⁶ 平方公尺那麼大面積的迴旋加速器。

解決的方法，要做兩件事情： (1) 讓質子在環狀軌道中行走，磁鐵僅需沿環狀路徑設置；(2) 加速循環的振盪頻率 fosc 與磁場 B 時時調整使之與質子運動同步化。如此，以費米 Lab 的加速器為例，其周長 6.3 km，質子能量達 1 TeV (10¹² eV)

作用在電流導線的磁力

由於 q = i t = i L / v_d

利用 F_B = q v × B，得

F_B = i L × B

如果導線並非直線，或是磁場並不均勻，則改考慮小段電流的受力再積分加總，

dF_B = i dL × B

作用於電流迴路的力矩

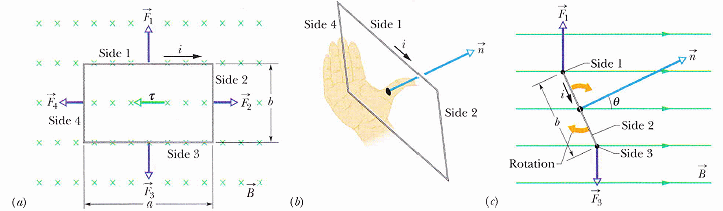
見圖，作用在電線上的力必定同時垂直於電線及磁場（右手定則），分析矩形的迴路，只有在轉動時永遠垂直於磁場的那兩段 a，其力的施力點及方向不會一在同一直線上，因而有力矩；另外，時時隨著轉動與磁場改變方向的那兩段電線 b，受力抵消。

τ' = (i a B b/2 sinθ) + (i a B b/2 sinθ) = i ab B b sinθ= i A B b sinθ

τ' = i A × B

雖然是從特例導出，但上面磁力矩與電流環路面積有關的公式是一般性的。

若線圈有 N 匝，則電流 N 倍

τ = N τ'

我們可以把這個系統看成磁場有磁力要把平面線圈的法向量 n^ 扭轉至平行於磁場。（這個觀點有助於我們看待感受磁力的物體）

 

 

磁偶極矩

μ = N i A

τ = μ × B

比較電偶極位能（請見前面章之推導）的

U(θ) = - p · E

磁偶極（磁矩）在磁場中的位能是

U(θ) = -μ· B

ΔU = U_f - U_i

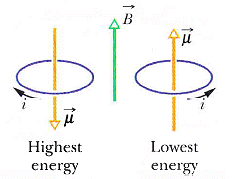
不只是電流迴路，一個磁鐵棒、地球地磁、很多基本粒子，包括電子、質子、中子，也都具有磁偶極矩。

 

電流所產生的磁場

必歐－沙伐定律

由實驗得知，一小段電流元素在空間中建立的磁場是

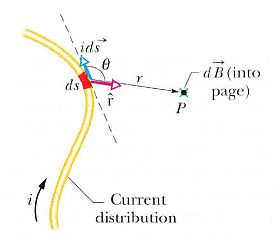
dB = (μ₀ / 4π) i ds × r^ / r²

其中 μ₀ 是磁導率（μ= μ₀ (1+ χ_v)，其中 χ_v volume magnetic suscpetibility 又叫體磁納係數）

以下是一系列簡單電流幾何所產生的磁場

 

長直導線電流產生的磁場

B = μ₀ i / 2πR

其中 R 是空間點與直導線的最近距離（推導見課本）

右手握導線、姆指指向電流，四指彎成磁場。

 

圓孤導線電流在圓心產生的磁場

B = μ₀ i Φ / 4 πR

其中 Φ 是圓幅角度、R 是半徑

 

腦部活動產生的磁場

量測點在腦部表面溝之壁上方兩公分的高度，神經電流 10 mu A ，通導路線約 1mm，當成小線段 ds，磁場大約 3 × 10^-12 T (即 3 pT)

需要 SQUID 裝置

兩平行電流間的力

算出一條電流在另一條位置上的磁場，再用 q v B （即 i L B）算出導線上的力。

F_ab = μ₀ L i_a i_b / 2 π d

其中 L 是導線長度、 i_a 與 i_b 各是電流，d 是間隔。

力為什麼不會不一樣？由於電流出現在磁場公式與磁力公式中都是分子一次方，因此兩條線上的力是對稱的。（從作用與反作用來想也可以）

平行電流相吸，反平行電流相斥。

 

電磁軌道發射槍

 

安培定律

小量電荷元素的靜電場有庫倫定律，非常複雜們分佈用電腦處理，至於較對稱的電荷分佈則有高斯定律可利用。同樣的，小電流元素有必歐－沙伐定律來預測空間中處處的磁場，非常複雜們分佈一樣得用電腦處理，對於高度對稱的電流分佈，我們則有安培定律來幫忙簡化：

∫_CL B · ds = μ₀ i_enc

其中 積分範圍是封閉迴路 (Closed Loop) ， i_enc 是迴路中的淨電流。

 

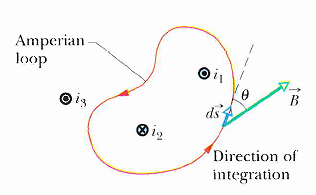
以下是各種電流幾何的例子：

 

載電流長直導線的外部電場

∫_CL B · ds = B ∫_CL ds = B (2πr) = μ₀ i

B = μ₀ i / 2πr

 

載電流長直導線的內部電場

假設內部電流密度均勻，則姑妄培定律給出

B (2πr) = μ₀ i (π r² / π R²)

B = ( μ₀ i / 2πR²) r

其中 R 是長直導線半徑，r 是與軸心距離。

 

螺線管 (Solenoid) 與 螺線環 (Toroid)

螺線管的磁場

見圖 FIG.29-18, 19, 20

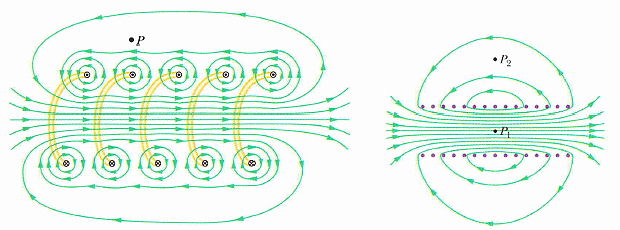
B = μ₀ i n

n 是單位長度之匝數 (number of turns)

 

螺線環的磁場

見圖 FIG.29-21

B = ( μ₀ i N / 2 π ) ( 1 / r )

可被視為磁偶極的載流線圈

前面已討論過，線圈的磁偶極矩 μ 是 來自 N i A 。（課本提醒大家別搞混 磁偶極矩 μ與 磁導率 或磁納率 μ₀ ）

對於圓環迴路軸心 z 處的磁場大小是（由於對稱性較少，無法用安培定律，而是使用必歐－沙伐定律來處理（過程見課本），如下：

B(z) = μ₀ i R² / [2 (R² + r²)^3/2]

若在相當遠處，即 z >> R，可進一步簡化為

B(z) = (μ₀ / 2π) μ/ z³

偶極對場之矩離的的三次方反比率又再次出現。

例題：

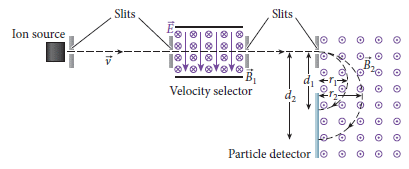
28-3 質譜儀

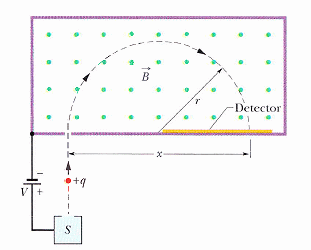
28-7 電表

29-1

29-2

29-3