電容、電阻與電路

 

電容

電容器 (capacitors)

 

電容 Capacitance

q = C V

電容 C 的意義是，多少電荷的注入（或說分離），才能讓電容器 (capacitor) 的電位提昇一伏特。

從另一個角度來說，電容器是貯存電能（當然也是電荷）的元件，它是透過在空間中建立電場的方式達到（這是需要花費能量代價的）。

C 只與裝置的幾何有關。以平板電容為例，電容值與板的帶電量及板之間的電位差無關。

 

電容的計算

策略想法

電容是貯存電荷的元件，而有電荷就會有電場，因此造成電位差。如此，q = C V 的 q 與 V 就有了，可得 C。

（事實上，在電腦 RAM 的原理上，電容若目的就是貯存電荷以建立電位，見 "科技的原理 1, 2 "）

思考：除了配置電荷之外，有沒有其他辦法在空間中，建立靜電場（與時間無關的電場）？

 

先計算電場

使用高斯定律，利用對稱性的討論，求出裝置中電場與電荷之間的關係。

 

再計算電位差

以電場對距離積分獲得電位差。如此則得到電位差與電荷之間的關係。

 

利用 q = C V，看給入 q 可以在該裝置中建立多少 V，則可定出 C 。

 

幾個電容器之電容值計算的範例：

（課本中有詳細推導，請自行確實練習）

平行板電容器

C = ε0 A / d

其中 A 是平板面積、d 是間距。（對邊緣的電場有作理想化的近似，但面積大時也是不錯的近似。）

 

圓柱形電容器

C = 2πε0 L / ln(a/b)

柱長 L、內外徑 a、b

 

球形電容器

C = 4πε0 a / (1- a/b)

 

單獨球體

上式之 b → ∞，並假設內半徑 a = R

C = 4πε0 R

 

電容器的並聯與串聯

並聯

看圖 25-7 <22-7> ，並聯的電容器感受到同樣的電位差，不同電容器則各有其累積的電荷。合在一起看，則相當於，有一個電位差，造成 q1、q2、q3 的電荷分離。因此總和的電荷分離是

q = q1 + q2 + q3 = C1 V + C2 V + C3 V

= (C1 + C2 + C3) V = Ceq V

從比較我們可以看出

Ceq = C1 + C2 + C3

故並聯的電容器

Ceq = Σi=1n Ci

 

串聯

圖 25-8 <22-8>

分離的電荷量在每個串聯在一起電容器都一樣（因為在同一條電線上）， 而電壓降（即電位差）則由這些電容器分享。

1/Ceq = Σi=1n 1/Ci

 

儲存在電場中的能量

從作功的觀念來思考：

在一電容器上，己有 q' 電荷並建立了 V' 電位差，要再多移 dq 的微小電量作分離，則其位能變化為（微量電荷不造成位勢 V' 的變化）

dW = V' dq' = ( q' / C ) dq

W = ∫ dW = 1/C ∫0a q' dq' = q'2 / 2C

因此儲存的位能是

U = q2 / 2C

也可表示成

U = 1/2 C V2

帶電之電容器的電位能可視為是儲存在兩板間建立的電場

 

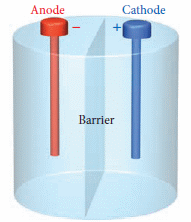
懸浮粉塵爆炸

（課文開章問題，如何防止）

已知懸浮粉塵到達爆炸的程度需最小火花能量約 150mJ （原因，能量規模小的點火，引起的燃燒規模尚不足以造成危險）。粉塵爆炸無法完全預防，故環安工程以限制電火花能量著手。將人視為身高大小的球形電容。根據公式算出帶靜電 4 萬伏左右即貯能達 150 mJ。因此廠內設置導電地板務使人員帶電總是遠小於此一數值以下。

 

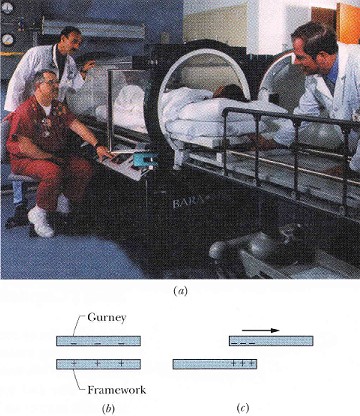
例題 25-4 燒燙傷用之高壓氧病床著火

 

能量密度

以平行板為例，能量密度

u = U / Ad = C V2 / 2Ad

因為 C = ε0 A / d ， 所以能量密度與電場的關係是：

u = 1/2 ε0 E2

以上給果在一般惰況也都正確，不僅限平行板電容器。

 

 

內含介電質之電容器

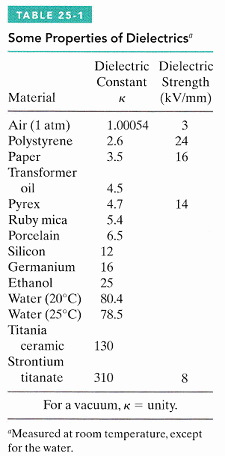
法拉第在 1837 年探討，若用非導體來填入電容的兩個板之間，電容值會怎樣變化？（法拉第的實驗見圖 25-12）

（因此電容單位以他命名）他實驗不同材料，以 κ 來代表填入後電容增加的倍數，他將之稱為該材料的介電常數。見表。

加入介電質的副作用是引入了能承受電位差的上限值，稱電崩潰電壓(位）Vmax，一旦超過則介電材料被破壞而形成通路，介電強度描述了承受外加電場的上限。

 

在填滿介電常數為κ 的介電材料的空間中，所有靜電公式中出現 ε0 者皆以 κε0 值取代即可獲得修正。

例如，點電荷在介電質中的電場

E = q / 4πκε0 r2

而帶面電荷密度的導體（不必是平板，因為電場必垂直於導體表面）與介電值接觸時，其表面外的電場值是

E = sigma / κε0

 

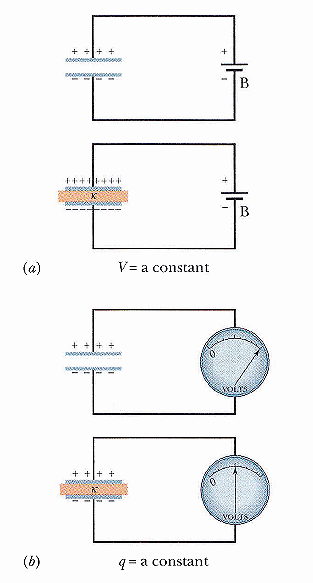
對於平行板電容，則有同理而有下列現象，(a) 固定電壓時蓄電量增加，或 (b) 固定電荷分離下電壓（電位差）減小：

為什麼會這樣？要從下一節微觀的圖像去了解。

問題討論：把介電值塞入上圖 (a)、(b) 兩種裝置中再移走，能量如何變化？需不需要作功？

 

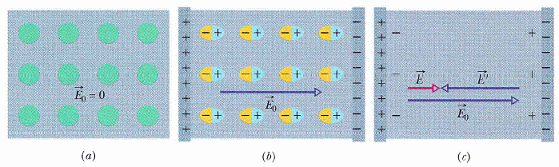
介電性的微觀圖像

極性介電質

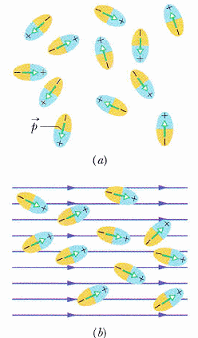
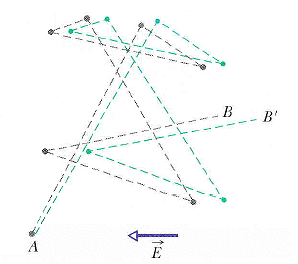
如水，水分子具有永久電偶極，平時混亂排列。圖 25-13

偶極排列會產生一個與外加電場方向相反的電場

（注意電偶極向量的定義，是由負電荷出發指向正電荷，而電場的定義則是由正電荷出發指向員電荷。如此定法，偶極向量平行於電場方向會降低總能。）

 

非極性介電質

靠著本身正負電荷受電場影響的暫時分離

 

電場（及電位）受到改變的機制

電偶極的排列或誘發使空間中的電場變小，這是因為，扣除了電偶極頭接尾抵消的效應後，還有面電荷分佈沒辦法抵消，而面電荷是會造成電場的（見圖 25-14）。

q = C V， V 變小，故 C 變大

 

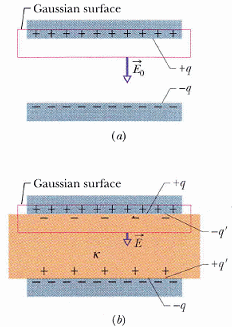
介電質與高斯定律

高斯定律仍然成立，但現在有面電荷出現，高斯面包住的淨電荷變少（圖 25-15）

，故電場變小。（注意原本公式是電通量正比於 q / ε0，在介質中 ε0 -> κε0）

我們在此想要的，是一個能寫出自由電荷與電場的高斯定律（誘發面電荷不方便處理與掌握）

以下推導：

原 ε0Φ = q，E0 = q / ε0 A

後 ε0Φ' = q - q' ，E = ( q - q' ) / ε0 A

而介電質使 電位（即電場乘以等長度）變小 1/κ 倍（才會這成電容值增為），即

E = E0 / κ

把前面兩式的 E0、E 代入，則有

q - q' = q / κ

得

κ( q - q' ) = q

而前已有

ε0Φ' = q - q'

代入上式，得

κΦ' = q

因此，高斯定律改寫為

ε0 ∫CS κE · dA = q

也就是說，在介電值中，一樣是 ε0 -> κε0 但為了處理不均勻質，κ移入積分中與 E 乘在一起較方便。

有些書籍把整個 ε0κE 叫做電位移 D，則有

∫CS D · dA = q

 

 

 

電阻

電流

要有淨的電荷移動才有電流效應

i = dq / dt

dq 是通過截面的電荷數

因為 q 與 t 都是純量，i 必定也是

 

電流密度

i = ∫ J · dA

若均勻

J = i / A

 

漂移速率

vd ≈ 10-5 or 10-4 m/s

v ≈ 106 m/s

J = n e vd

電場在導體內以接近光速進行

 

電阻 (Resistance) 與 電阻係數 (Resistivity)

定義

R = V / i

i = V / R

 

電阻係數

ρ = E / J

E = ρJ

上兩式在等向性 (isotropic) 材料成立，否則會是張量形式。

另定 傳導係數 (conductivity)

σ = 1/ ρ

 

由 電阻係數 來算 電阻

E = V/L

J = i/A

前有 ρ = E/J

故 ρ = E/J = (V/L) / (i/A) = VA/ iL = (V/i) A/L = R A/L

移項得

R = ρ L/A

 

隨溫度的變化

ρ - ρ0 = ρ0α(T - T0)

典型之金屬 ρ 值的溫度變化，見圖 23-9

 

歐姆定律

"通過一個元件的電流，與施加於元件的電位差成正比"

（雖叫 "定律" ，其實僅適用某些材料，這是歷史上的理由這樣叫。）

請注意，不應把 V = i R 叫做是歐姆定律，V = i R 是電阻的定義 R ≡ V / i

歐姆定律 是說， i 與 V 呈線性。

 

歐姆定律 的微觀圖像

推導漂移速率

電場造成的加速度

a = F/m = eE/m

在碰撞之前能獲得的速度就是漂移速度，來自平均自由時間內的加速

vd = a τ = eE τ/ m

己知

J = n e vd

故

vd = J / ne = e E τ/ m

整理出 E 與 J 間的關係

E = ( m / n e2 τ ) J

ρ = m / e2 n τ

若上述 ρ 是與外加電場無關，則 V 與 i 就會呈線性。在此 τ 與電場會無關的原因是，電場造成的漂移速率遠小於 veff，故 veff 及 τ 皆不受外加電場大小所影響。

vd ≈ 0.02 veff

 

電路的電功率

在時間 dt 內有 i dt = dq 那樣量的電荷流過迴路，而降了電壓，因此電位能差是

dU = V dq = V i dt

則功率為

dU/dt ≡ P = i V

表示成 R = V / i

P = i V = i2 R

也可表示成

P = V2 / R

以上的功率耗散都用於電阻性耗散 (resistive dissipation)

電力輸送線上無明顯壓降，但卻有某個電流大小，因此適用 P = i2 R 式，為了減少消耗，電流越小越好，故只得提高電壓 ( P = i V )，因此電力的輸送採取的是超高壓電。

思考：電阻大的燈泡與電阻小的比，那個亮？

 

半導體

利用摻雜後的多餘電子或電洞作載子。

電阻係數的溫度曲線與金屬不同，是越高溫導電性越好。

 

超導體

低溫下有些材料進入完全沒有電阻的狀態。

可絕磁，也可作強力磁鐵（取代電磁鐵）。

 

 

 

電流迴路

電路理論

 

Pumping charge

用電池

推而廣之可以是任何電動勢裝置。

 

功、能與電動勢

E = dW / dq

 

單迴路電路之電流計算

請注意我們這裏的目標是要算 "電流"

能量法

具電動勢 E 之電池對一微量電荷 dq 作功

dW = E dq = E i dt

此值，基於能量守恆，等於迴路上通過電阻的消耗

E i dt = i2 R dt

化簡之

E = i R

可解出現流

i = E / R

 

電位法

在迴路中以任意點為起點，位意方向環繞電路，把一路所遭遇之電差位加起來，直到回到出發點時（因為是迴路一定可以），電位也必須回到原來的值。也就是說（這叫克希荷夫迴路規則 Kirchhoff's loop rule）：

"在電路中，任一迴路的電位變化的代數和必為零"

以圖 24-3 之 a 點開始，

Va + E - i R = Va

因此

E - i R = 0

一樣可解出 i = E / R

以上使用了兩個規則

(1) 通過一個電阻，與電流方向相同，則電位變化 -iR，相反則 +iR

(2) 通過一個電動勢元件，方向相同，則電位變化 +E ，相反則 -E

 

兩點間電位差

通過真實電池的電位差

因為電池本身也有電阻

 

電路接地

接地處電位定為零

 

電功率、電位、電動勢

P = i V

P = i ( E - i r ) = i E - i2 r

Pemf = i E （電動勢作功）

Pr = i2 r （內部耗損）

 

多迴路電路

節點法則：流進任一節點的電流總和一定等於流出該節點的電流總和

示範：圖 27-9 的電路圖如何求電流 i1、i2、i3

電流方向可假設，反正解出後自有其正負號。

 

 

安培計與伏特計

安培計內含一小電阻，可量電流

伏特計量電位差，要有一個比被量線路大得多的電阻

可切換，為萬用電表

作業：安培計與伏特計的運作原理

 

 

RC 電路

在此被討論的電路見 圖 27-15

對電容充電

E - iR - q / C = 0

（電容是貯存能量的裝置，自然與電動勢反號）

基於 i = dq / dt ，故上式變成

R dq / dt + (1/C) q = E

此式又叫充電方程式，其解為 [對電容器充電的情況下] ：

q = C E ( 1 - e-t/RC )

又

i = dq /dt = ( E / R ) e-t/RC

 

時間常數

R C 乘積是一個常數，出現在指數次方之分母，單位是時間（寫在次方上的數必須無因次）因此是一個時間度量，每經過 RC 時間，大小成為原來的 e-1 = 0.37 倍。

 

電容的放電

與上式同，但無電動勢

R dq / dt + (1/C) q = 0 （放電方程式）

其解為

q = q0 e-t/RC

i = dq /dt = -( q0 / RC ) e-t/RC

 

 

EX-150

http://www.youtube.com/watch?v=6r98FZq2A4I

http://www.youtube.com/watch?v=iNfTL3Kw4hQ

 

範例

22-4

23-3

23-4

23-5

24-2

24-3

24-4

全華 25-7

全華 27-3

全華 27-4 電鰻