高斯定律與電位（勢）

高斯定律與電場

對稱性的利用

利用對稱性，可簡化某些計算

高斯提出高斯定律，把電場的面積分與電荷分佈關聯起來。

 

通量

Φ = v cos θ A = v · A

曲面上的一小塊，可視為平面，故有明確之法線方向，可作為內積時代表該小面積單元的方向。（夾角零度相當於向量平行，故結果場強度直接相乘於面積，夾角 90 度則乘積為零，任意角度則是投影，恰符合 cos θ 的定義）

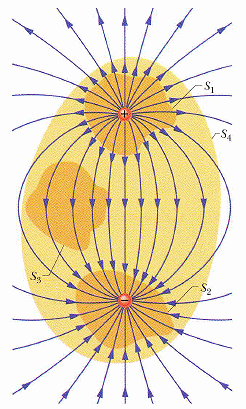
示意圖 23-2 （或另一書之圖 20-2）

 

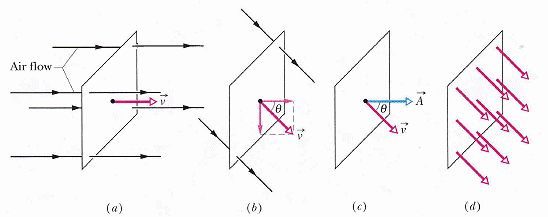
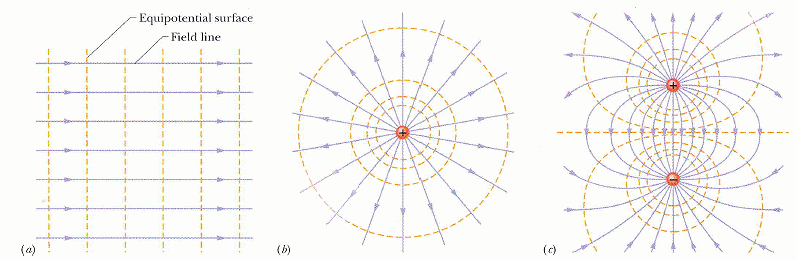
電場的通量

Φ = ∫_CS E · dA

電場是單位面積的電力線數，乘上面積後是總電力線數。

通過高斯曲面的電通量 Φ 可視為是通過此曲面的電力線之總數。又由於電力線源自電荷，因此，封閉曲面電通量和正比於曲面所包覆淨電荷。

 

高斯定律

ε₀ ∫_CS E · dA = q_enc

積分中之下標 CS 代表 Close Surface ，即封閉曲面。

 

高斯定律 與 庫倫定律

由高斯定律推導出庫倫定律

ε₀ E (4 π r²) = q

故

E = (1 / 4πε₀) q / r²

 

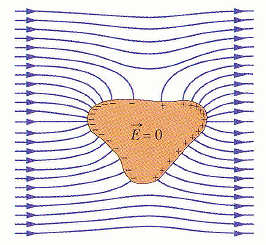
帶電孤立導體

若將額外電荷置導體上，則這些電荷全數移至導之表面，而且導體的內部完全無電荷。

以上陳述可用高斯定律證明：

（圖 20-9 自行閱讀）

 

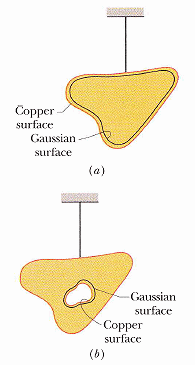
具空腔的孤立導體

空腔壁上無淨電荷

思考：打洞串通圖 (b) 會怎樣？

 

嵌入電荷再移除導體

 

（局部）導體表面的電場

E = σ / ε₀

 

 

 

高斯定律的深刻內涵

一個東西的特徵僅由表面決定，則其體內單元必定有一些特殊的簡化（單）條件。

本節我們使用高斯定律的積分型

ε₀ ∫_CS E · dA = q_enc

其實，等效於下列的微分形式：

∇· E  = ρ / ε₀

其中 ρ是電荷密度分佈函數。

高斯定律的應用（自行閱讀，及助教示範）

圓柱對稱

圖 23-14 "好玩的體驗？"

 

平面對稱

非導體平板

兩導體板

 

球對稱

證明球殼定理

 

上列這些理想的情況常是不錯的近似。

電位 (勢)

電力是否為保守力？

若是，則它可用作功的觀念建立位能而與守恆量連接起來，對我們討論與預測都非常方便。

電力的確是保守力

 

電位能

ΔU = U_f - U_i = -W

注意保守力作功與位能之間是有負號的。

對帶系統一般定各帶電粒子相距無限遠為位能參考點。若令 Ui 為零，則

 

電位

V = U / q

 

等位面

空間中所有電位相同之點所構成之面

從做功要有值的觀念去推理，"任何地方電場永遠垂直於等位面"

 

從電場算電位（差）

dW = F · ds

F =q₀ E

 

V_f - V_i = - q₀∫_i^f E · ds

若定 Vi 為零

V = - ∫_i^f E · ds

 

點電荷的電位

V = k q / r

k = (4 π ε₀)^-1

 

一群電荷的電位

V = k Σ_i q_i / r_i

 

一個電偶極的電場

V = k p cos θ / r²

其中 p 是 diploe， θ是夾角如圖 24-10。

 

連續電荷分佈的電位

V = ∫ dV = k ∫ dq / r

 

從電位算電場

E_s = -∂V / ∂s

向量表法之最一般形式

E = -∇V

 

 

點電荷系統的電位能

一樣定無窮遠距離為位能零點，故位能為，形成目前固定電荷分佈組態，外界所需做的功。

U = k q₁ q₂ / r

 

孤立帶電導體的電位

內部常數（因為電場為零），見例圖 24-18

 

帶電導體的放電

躲在導體殼內的表演、內部沒事。

 

外加電場下的孤立導體

導致電場垂直於導體表面，如圖 24-20。

作業：解釋電漿球 (Plamsa Ball) 玩具的運作原理

http://en.wikipedia.org/wiki/Plasma_globe

例題：

23-1

23-2

23-3

23-4

23-5

23-6

23-7

24-6

24-7

 

明年是發現超導及宇宙射線一百年