電荷與靜電
摩擦生電的組合
玻璃棒、絲(絹):棒帶正電
塑膠棒、毛(皮、毛料):棒帶負電
銅棒、羊毛:銅棒帶負電
范德格拉夫發電機 http://www.youtube.com/watch?v=1jP_D0S2CtY&NR=1
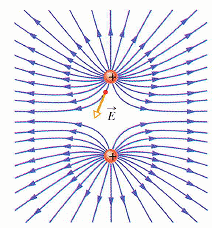
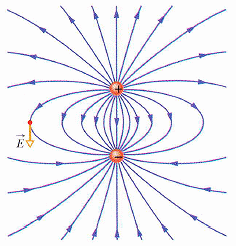
用懸吊的玻璃棒、塑膠棒做實驗,可以得到 "同性相斥、異性相吸" 的結論。
電的正與負由富蘭克林命名,完全是任意的,也就是說反過來定也沒有錯。
導體與絕緣體
物質由原子構成、原子核帶正電、電子帶負電
導體的內部,有一小部分受束縛較小的電子,可以在導體的內部自由移動,也就是說,正電荷的表現在一般固體是因為負電的移走,如此也就決定了正電荷在固體中是固定的這樣的事實。
感應電荷
物質中同時帶有大量但等量的電荷而維持中性
即便一個中性的金屬棒,在帶電體接近時,也會因同性相斥的關係,導體內的同性電被排開(或異性電被吸引過來,取決於帶正體是正或負)
會發光的 Wintergreen Lifesaver 糖果
http://chowhound.chow.com/topics/398644
http://recipes.howstuffworks.com/question505.htm
http://www.highlightskids.com/Science/TryThis/h3TT1205_candySparks.asp
細菌感染與靜電學
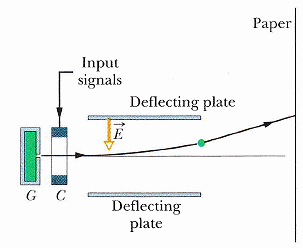
映像管螢幕會吸附灰塵(機制見課文)
醫事人員被提提醒勿以(戴膠手套的)手,近距離去指著螢幕討論。
電力:庫倫定律
兩個點電荷間的作用力是:
F = k | q1| | q2| r^ / r2
其中 r^ 是方向向量。
這個公式同時適用於 q1、q2 兩個點電荷,描述它們的受力。描述 q1 時,就以 為中心,則 F 向量正確地表示出 q1 的受力大小及方向。描述 q2 時,也是同理。
與 萬有引力公式 的相似性
庫倫定律公式 與 萬有引力公式 在形式上完全一樣
F = G m1 m 2 r^ / r2
其中 G 是重力常數,因此庫倫定律中的 k 也叫作是靜電常數。
k = 1/ (4πε0) 也是一種常用的表示法(有時能簡化公式),其中ε0 是真空電允率 (permmitivity constants)。
重力與靜電力都滿足疊加性原理,多個點電荷對某電荷的力,可由各別電荷對的結果兩兩加起來。
又,由於與重力公式的相似性,也因此,之前學過之萬有引力的性質也可以用在靜電問題上,如球殼定理:
(1) 均勻電荷分佈的球殼,對其外之電荷而言,作用力相當於集中於球中心點。
(2) 對球殼內無靜電力作用。
球形導體
將額外電荷置於球形導體上,淨電荷將會均勻分佈,故根之球殼定理,
電流:安培與庫倫
電荷的 SI 制單位是庫倫,但 SI 制 六大基本的量中與電有關的是電流(單位:安培)而非電荷,這是因為電流較容易精密測量的關係
i = dq / dt
一庫倫等於一安培電流在一秒鐘流過的電荷量。
基本電荷(電荷的量子化)
此量子化並不是一般講量子化的能量之量子化,而是電荷大小的量子化,即基本電荷有其最小的單位 e,即電子所帶的負電量或質子所帶的電量。
密立根設計出著名的油滴實驗,量得電荷的基本單位( 1.60 × 10-19 庫倫),後面還有介紹。
電荷守恆
富蘭克林首先提出,電荷守恆假說,現己成為電荷守恆定律(另有線動量守恆、角動量守恆,以及能量守恆三種定律)。經過許多審慎的檢驗,大型帶電體及原子、原子核等基本粒子,皆未有違反此一假說者。(微中子的發現)
兩例:
(1) 核衰變過程中的電荷守恆
238U → 234Th + 4He
(Th 是 "釷")alpha 粒子是 He 的核。U (92+), Th (90+), He (2+) 故電荷守恆
(2) 正、反粒子對生及對滅過程中的電荷守恆
γ→ e- + e+ (對生 creation,見圖 21-11)
e- + e+ → γ + γ(對滅 anihilation)