簡諧振盪的運動方程式
對時間微分兩次
微分方程式(運動方程式)
d2 x(t) /dt2 = - k/m x(t)
也就是說,綁在(質量可略不計之)彈簧上 的物體的運動行為,其中 ω = √(k/M)
位能
U = (1/2) ω x2
簡諧運動之重要性
任何回復力位勢在接近平衡點處都是拋物線形,也就是一次方力。(數學上可證明函在極值處由於斜率為零,泰勒展開由平方項開始,故有上述性質。)複習:泰勒展開式。
振盪:簡諧運動、阻尼與共振
簡諧運動
簡諧運動的定義
x(t) = A0 sin(ωt + φ)
其中
A0 是振幅
ω是角頻率,1/ (2 π ω) = T 是週期
φ是相位角
複數的表示法也很常見
x(t) = A0 ei(ωt + φ)
其中 eiθ = cos(θ) + i sin(θ)
ei(ωt + φ) = cos(ωt + φ) + i sin(ωt + φ)
簡諧運動的軌跡
一維情況
兩個獨立 SHG 圖形之組合:李沙育圖形
Ax, Ay, ωx, ωy, δx, δy 皆不同
簡諧振盪的運動方程式
對時間微分兩次
微分方程式(運動方程式)
d2 x(t) /dt2 = - k/m x(t)
也就是說,綁在(質量可略不計之)彈簧上 的物體的運動行為,其中 ω = √(k/M)
位能
U = (1/2) ω x2
簡諧運動之重要性
任何回復力位勢在接近平衡點處都是拋物線形,也就是一次方力。(數學上可證明函在極值處由於斜率為零,泰勒展開由平方項開始,故有上述性質。)複習:泰勒展開式。
多質點系統之的振盪的基本模式(Normal Mode)
維基百科 http://en.wikipedia.org/wiki/Normal_mode
C2H6 分子之 normal modes 的其中三種
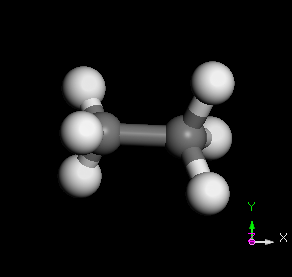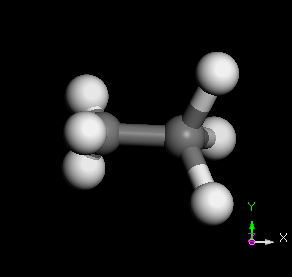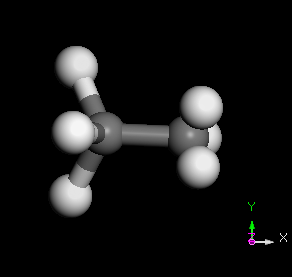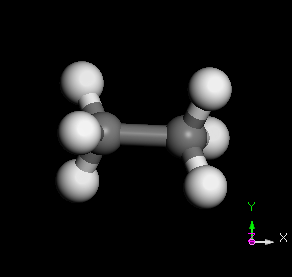
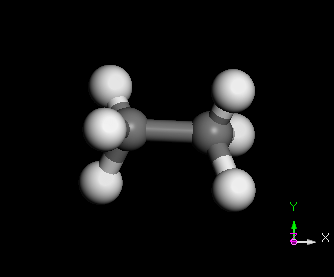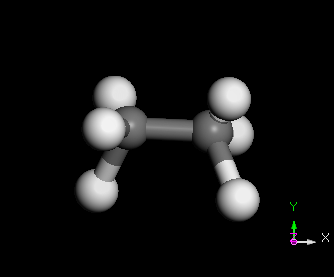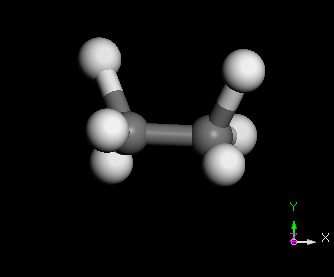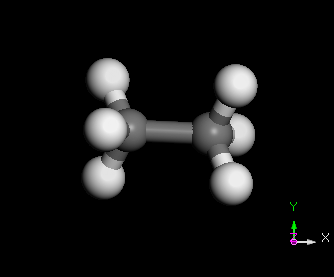
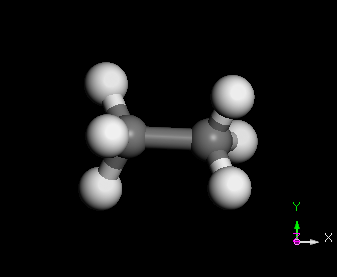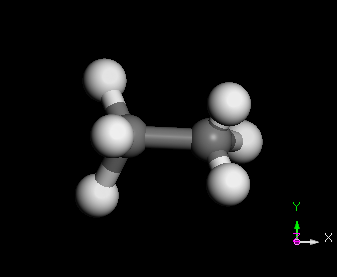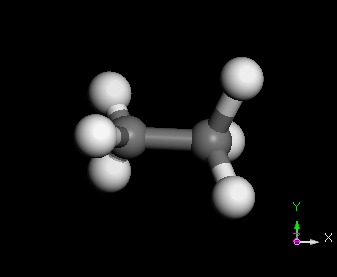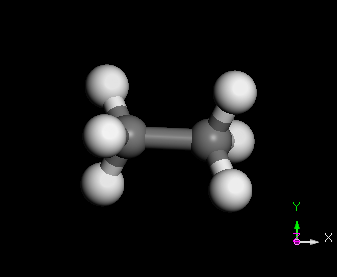
幾種常見的簡諧運動裝置
彈簧
扭擺
Fig 15-7
τ = - κ θ
簡單鐘擺(單擺)
真實(物理)擺
也有翻譯作複擺
週期是 (15-29) 式
可利用複擺來精密量測 g 值
g 值是 (15-31) 式(單擺公式裏的 g 消掉所以不能求 g)
均勻(等速)圓周運動的投影
阻尼
阻力
是一種消耗力學能(機械能)的過程,與速度有關,例如下圖裝置
Fd = - b v
代入 Fnet = m a,得
- b v - k x = m a
受阻尼簡諧運動方程式的解
解微分方程式
-bv - k x = ma
m d2 x/dt2 + b dx/dt + kx = 0
通解為
x(t) = A0 e -bt/2m cos(ω't + φ)
有新的角頻率
ω' = ( k/m - b2/4m )(1/2)
而重要的是隨時間指數衰減的因子,要套在振幅上
e -bt/2m A0cos(ω't + φ)
將造成 under damping, over damping, critical damping 等現象
以 under dampling 即 b < √(km) 為例
數值的電腦模擬
也可以很方便地用電腦模擬出來
施力振盪 與 共振
施力振盪 (forcaed oscillation)
有外力的
瞬間外力
用衝量處理,換成初速度
週期外力
當驅動力頻率 ωd 等於振盪系統的自然頻率 ω 時,振幅會越來越大。直到被阻尼抵消而達到最大值。
隨機外力