幾何光學

看見影像

能夠把外界事物映射 (map) 到神經知覺系統的能力

生物中，原始簡單眼點只能感應明暗

精密的視覺可以看見幾公里外的小東西的形體

 

光線：光（走直）線

遠物看似小、近物看似大

光學很早就與三角、直線等幾何學結合在一起

（光線也是一種想像的圖像，但比電力、磁力線早，也簡單）

 

光的交叉

任兩道光在交叉後，各自方向不受影響，繼續前進（這個部分是波性質）。

思考：來自同一個點光源的光線，若有機會交會在一點，

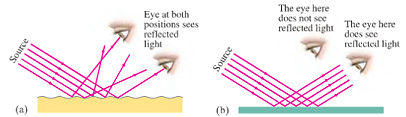
反射 與 看見影像

思考：既然如此，教室開前門，為何黑板上不呈現走廊上的人之影像？

成像

何謂成像？

一個物體上發射或反射出來的光只會到達屏幕上的唯一一點，且相鄰的點會映射在相鄰的區域，就叫作（在該屏幕上）成像。（也就是說，像上的任一點，都只能接受來自物上的某同一個點的光線，這就是成像的條件。哈哈鏡也符合此一條件。）

（正確的比例只並不重要，大腦會自行修正或忽視，或僅取用需要的資訊而不會感到奇怪。如新配眼鏡不適應視線週圍的曲折度。）

因此，不失去一般性的情況之下，成像的定量探討只需考慮物距 d 與物高 h 即可。（整個幾何光學的光跡追蹤 (ray tracing) 之探討都會用這種方式）

 

針孔相機的成像

光的反射與折射

為了計算與預測影像的捕捉與放大（成像），要尋求光線行進的幾何公式（即幾何光學）。

實驗很容易觀察到，理解由惠更斯原理：波前上的每一點都是新點的光源。如此可解釋反射與折射。

（另外，從最速路徑的原理也可推出反射與折射的結論）

 

光跡追蹤：以平面鏡反射為例

 從 "光走直線" 的觀點出發，追蹤三條光線，找新的交會（成像）點：

1.（頂點光源）平行

2.（頂點光源）射向中心

3. 光軸

 

如此可得出

h_o = h_i

| d_o | = | d_i |

反射

公式：入射角等於反射角

 

常見問題：穿衣鏡要怎麼配才看得到全身

例題 32.1： 穿衣鏡

 

球面鏡

 

f = R / 2

 

球面相差

 

拋物面鏡

拋物面鏡不會有如球面鏡那樣的像差問題，但也較難製造

對於一個拋物線，y(x) = a x² 所構成的鏡面，它的焦點位於

f = a / 4

新技術：拋物液面鏡

折射

折射率：光在透明介質中傳播速度不同的程度（相對於真空，其折射率是 1.0）

由光速在真空與介質中的不同來定義該介質的折射率：

n = c / v

其中 c 是真空中的光速、v 是介質中的光速。

密度大的介質折射率大，密度小的介質折射率小。

 

司涅耳定律 (Snell's Law)

定法線方向的角度為零，則

n₁ sin θ₁ = n₂ sin θ₂

 

全反射

光從密介質到疏介質，出射角大於入射角，有機會造成出射角大於 90 度，於是不射出。

例：鑽石與光纖。

 

光纖的應用

通訊

http://163.13.111.54/science_works/Page046_Cable_technology_01.jpg

商用光纖採用玻璃 (SiO2) 纖維摻鍺以提高折射率。

LED 發出來的脈沖光（數位：0 與 1）訊號可傳約 500 公尺而無明顯衰減，每隔 500 公尺要作接收、放大再續傳。

 

內視鏡

一堆細光纖可以束在一起，仍不至於過粗而可以作為內視鏡的導光骨幹而伸入體內，每條光纖是一個畫素，約有 7000 至 25000 畫素。

 

反射引起的偏極化

布魯斯特角，發生在入射線與反射線垂直時（原因？），此時反射線完全呈水平偏振。

配帶偏光眼晴，有助於釣魚及駕車時避免眩光，閱讀也是。

透過緩慢旋轉的偏光片來看書本印刷油墨所發出來的炫光（教室現場自製影片，點擊下圖即可撥放）