在沒有介電質或磁性質存在的情況下,四條方程式整理如 表 32-1 :
高斯定律
磁學高斯定律
法拉第感應定律
安培-馬克斯威爾定律
馬克斯威爾方程式(組)也有微分型式
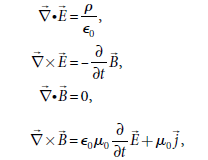
這四個一組的方程式描述所有巨觀的磁、電、光現象,甚至光的速度也藏在其中。固定的光速值還引發了近代物理的新革命。
透過微分型 Maxwell's Equations 的推導整理,可得知電場與磁場各自需滿足(特徵是同時具有對空間兩次微分與對時間兩次微分的)波動方程式 :
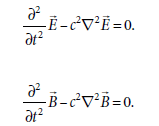
推導方式如下:

馬克斯威爾方程式 與電磁波
馬克斯威爾方程式
磁場的高斯定律
磁單極(目前所知)並不存在
ΦB = ∫CS B · dA = 0
比較電場的高斯定律
ΦE = ∫CS E · dA = qenc / ε0
磁折成幾段,每一段都變成磁鐵,各自有 N、S 極,如圖 32-2
討論題:所以,打斷的磁鐵,應該自已可以吸在一起而保持原來的形狀,對嗎?
感應產生的磁場 (Induced Magnetic Fields)
法拉第感應定律是 "磁變生電"
∫CL E · ds = - dΦB / dt
而馬克斯威爾感應定律則是 "電變生磁"
∫CL B· ds = μ0ε0 dΦE / dt
實驗證明的確如此。
這種感應的一個特殊例子是正在充電中的電容器
安培-馬克斯威爾定律
回憶安培定律
∫CL B · ds = μ0 ienc
而前一小節的馬克斯威爾感應定律等號左邊,也出現同樣的磁場環路積分,我們可以合併這兩個方程式:
∫CL B · ds = μ0ε0 dΦE / dt + μ0 ienc
稱為 安培-馬克斯威爾定律
位移電流
這是馬克斯威爾最後統合四條一組方程式的最後一塊拼圖(達成公式的美麗與完整)(為什麼?因為電與磁的地位對稱,也因為波動方程式才推導得出來,見下)。我們看上面的 安培-馬克斯威爾定律之等號右邊的兩項,而設想一假想電流,位移電流
id = ε0 dΦE / dt
則
∫CL B · ds = μ0 id,enc + μ0 ienc
如此,就都可用電流源來理解磁環路。
位移電流的物理意義
變動中的電場,可視為電容上的充電電荷正在變化數量(因此電力線的數目也才會變化),而能造成電容充電的,正是電流。此電流不是真有電荷傳輸過去,而是累積在電容器上的電荷分離,因此才叫電位移。故造成類似電容器充電的充電效應的假想電流,叫位移電流。
求感應磁場
對半徑 R,正在充電的平板電容,我們可用 id 來求感應磁場的大小,電容之內距中心為 r 的點其磁場大小為,
B = (μ0 id / 2πR2) r
在電容器外則是
B = μ0 id / 2πr
馬克斯威爾方程式(組)
在沒有介電質或磁性質存在的情況下,四條方程式整理如 表 32-1 :
高斯定律
磁學高斯定律
法拉第感應定律
安培-馬克斯威爾定律
馬克斯威爾方程式(組)也有微分型式
這四個一組的方程式描述所有巨觀的磁、電、光現象,甚至光的速度也藏在其中。固定的光速值還引發了近代物理的新革命。
透過微分型 Maxwell's Equations 的推導整理,可得知電場與磁場各自需滿足(特徵是同時具有對空間兩次微分與對時間兩次微分的)波動方程式 :
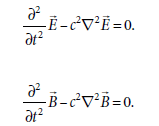
推導方式如下:
電磁波
馬克斯威爾的彩虹
馬克斯威爾的重大成就是證明了光就是電場與磁場所形成的電磁波。
行進電磁波的的定性分析
產生行進電磁波的裝置
見圖 33-3,一個 RLC 電路並配合天線,就能夠發射電磁波。
行進電磁波的重要特徵
1. E、B 各自垂直於行進方向
2. E、B 互相垂直
3. E × B 即是波行進的方向
4. 場總是依正弦型式在改變
E = Em sin(kx - ωt)
B = Bm sin(kx - ωt)
波速
c = 1 / √(μ0ε0)
E / B = c
一個最難以理解的波
電磁波並沒有(不需要)傳播的媒介,光速在所有座標系中都之一樣的值。它與時間一起,是時空間結構的一部分。
行進電磁波的的定量分析
電場與磁場們雙重感應可提供我們光。
推導 Em / Bm = c
在 dx 的距離之兩端,電場為 E 與 E + dE,取 h 作長而與 dx 的寬形成的面積裏,討論該面積迴路中的感應磁場,利用法拉第定律
∫CL E · ds = − dΦB / dt
∫CL E · ds = ( E + dE ) h - E h = h dE
ΦB = ( B ) ( h dx ),故
dΦB / dt = h dx dB/dt
代入法拉第定律,得
h dE = - h dx dB/dt
即 dE / dx = -dB / dt
事實上,E、B 皆為時間與空間的函數,上式應作
∂E / ∂x = -∂B / ∂t
我們把 E = Em sin(kx - ωt) 及 B = Bm sin(kx - ωt) 當作是己知,則有
∂E / ∂x = k Em cos(kx - ωt)
∂B / ∂t = - ωBm cos(kx - ωt)
故有
k Em cos(kx - ωt) = ωBm cos(kx - ωt)
k Em = ωBm
我們知道行進波的波速(相速度)是 ω/ k ,故
Em / Bm = ω/ k = c
推導 c = 1 / √(μ0ε0)
見課文
圖 33-7
討論 dx 範圍兩側的磁場值 B 與 B + dB,利用磁場環路積分與電通量變化關係的 安培-馬克斯威爾感應定律
∫CL B · ds = ε0 μ0 dΦE / dt
∫CL B · ds = - (B + dB) h + B h = -h dB
請注意由於迴路方向的設定,上式的第一項是負的
ΦE = ( E ) (h dx)
對上式微分
dΦE / dt = h dx (dE / dt)
另外注意 上式對時間微分不會作用到 dx,因為這裏探討的函數是場,對場而言 x 只是空間的舞台自變數,不像是粒子的軌跡函數 x(t) 那樣。
全部代入安培-馬克斯威爾定律,得
-h dB = ε0 μ0 h dx (dE / dt)
-∂B / ∂x = ε0 μ0 ∂E / ∂t
現在代入 B、E 的行進波的正弦函數
- k Bm cos(kx - ωt) = -ε0 μ0 ωEm cos(kx - ωt)
k Bm = ε0 μ0 ωEm
Em / Bm = 1/ ( ε0 μ0 (ω/k) ) = (1/ ε0μ0 ) (1/ ( ω/ k ) ) = 1/ ε0μ0 c
由前面己知的 Em / Bm = c,則得
c = 1 / √ ε0μ0
(從這裏你可以看到,光速就藏在馬克斯威爾方程式組裏。光速的測量,可以分別做電容及電感實驗來量到。)
能量傳輸與波印亭向量
S = 1 / μ0 E × B
S = 1 / μ0 E B
因為 E / B = c
S = 1/(cμ0) E2
以上是瞬間的能量流率
I = Savg = 1/(cμ0) [ E2 ]avg = 1/(cμ0) [ Em2 sin2(kx - ωt) ]avg
Erms = Em / √2
I = 1/(cμ0) Erms2
問,這裏面電場佔大部分嗎?
由電場的能量密度出發展開
uE = 1/2 ε0 E2 = 1/2 ε0 (cB)2 = 1/2 ε0 c2 B2 = 1/(2μ0) B2 = uB
恰好等於磁場能量密。因此,這裏面的電場能量密度與磁場能量密度是一樣大的。
強度隨著距離而改變
一個真實的電磁幅射源,其強度隨距離的變化是複離的
基於能量守恆,考慮為點光源
強度 = 功率 / 面積 = Ps / 4 π r2
光之幅射壓
光不但有能量,也有動量。(沒質量的東西也可以有有動量?在相對論申會再說明。)
完全吸收所造成的動量改變
Δp = ΔU / c
沿原路徑所造成的動量改變
Δp = 2 ΔU / c
若是部分吸收部分反射,則動量改變介於上兩者之間。
由牛頓定律,動量變化與力之間的關係為
F = Δp / Δt
另外,為表稍後要以幅射強度 I 來表示幅射壓,請注意強度是
強度 = 功率/面積 = (能量/時間)/面積
故有
ΔU = I A Δt
則,對完全吸收
F = Δp / Δt = ΔU / ( c Δt ) = I A Δt / ( c Δt ) = I A / c
對完全反射
F = Δp / Δt = 2 ΔU / ( c Δt ) = 2 I A Δt / ( c Δt ) = 2 I A / c
則幅射壓,對完全吸收為
pr = I / c
對完全反射
pr = 2 I / c
幅射壓玩具 Radiometer
波長與阻隔的關係
微波爐的門的功能。
偏振
電場是在一個平面上振盪,見圖 33-9
偏振光
電視臺發出的電磁波有特定偏振方向,一般光源或日光則是隨機偏振,也叫非偏振
可藉由通過偏振片而把非偏振光變成部分或完全偏振光,此因偏振片上有排列整理如犁溝的長鏈分子。
穿透之偏振光的強度
I = I0 / 2
對己偏振的光而言,若 θ 為與偏振片允許電場通過方向之夾角
Ey = E cosθ
I = I0 cos2θ
見 例題 33-2 之圖
偏光片的生活應用
3D 電影
釣魚、開車用太陽眼鏡
透過緩慢旋轉的偏光片來看書本印刷油墨所發出來的炫光(教室現場自製影片,點擊下圖即可撥放)
旋光性與糖度檢測
糖分子有旋性(如左右手有鏡像性稱,但左右手卻不一樣)
電磁幅射傷害?
http://tepca.blogspot.tw/2010/08/blog-post.html