電磁振盪 與 電流

 

 

LC 電路

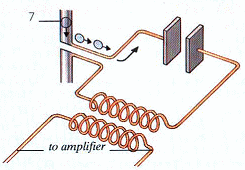
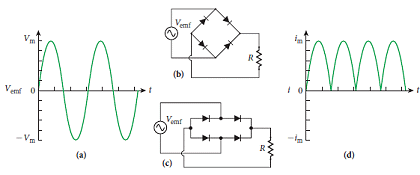
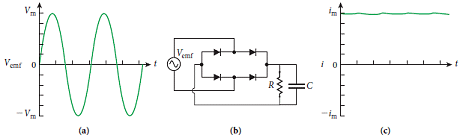
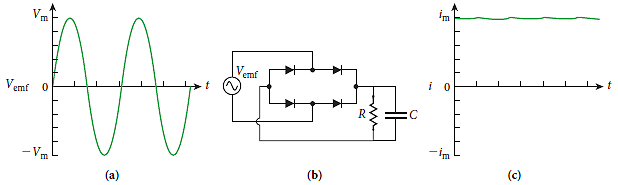
貯存電能（電荷）的電容元件與建立磁場

 

 

LC 振盪的定量分析

質量塊－彈簧振盪器

此系統任一時刻總能是

U = Ub + Us = 1/2 m v2 + 1/2 k x2

這是一個與時間無關的常數，故其對時間的一階導數為零。對上式作對時間微分一次並令為零，並利用 v = dx/dt 、dv/dt = d2x/dt2 的既有關係，得到運動方程式

d2x / dt2 + k/m x = 0

上式的通解是

x = X cos(ωt + φ)

 

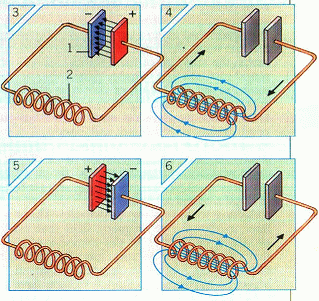
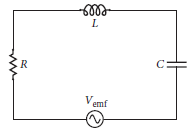
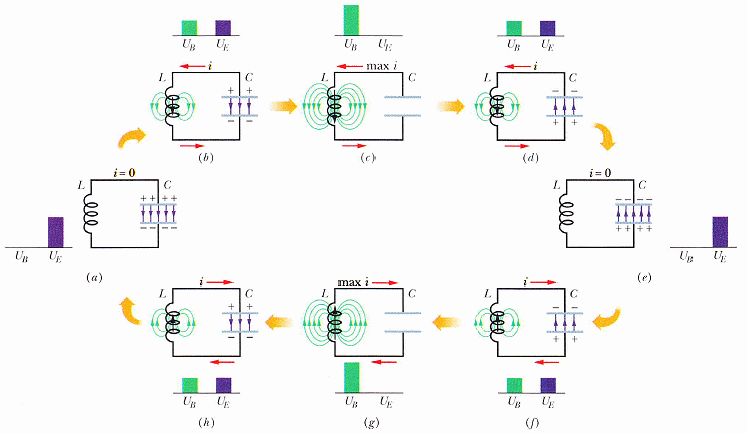
LC 振盪器

U = UB + UE = 1/2 L i2 + q2 /2C

dU / dt := 0 （令為零）

d2q / dt2 + (1/LC) q = 0

（回想彈簧質量塊系統：d2x/dt2 + (k/m) x = 0）

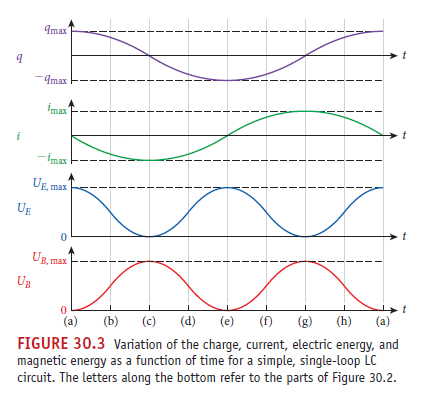
其解的時間函數變化如下：

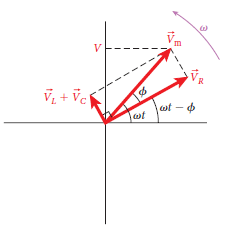
通解形式 q(t) = qmax cos( ω0 t - φ)

 

解出之角頻率

ω0 = 1/ √(LC)

 

觀察

電荷值 q 乘上電位就是電能作功 （不是電位能），因此電荷就像力學問題中之位置。

電流 i 好像速度，與摩擦力(耗能)有關。

則 di/dt 就相當於力學問題中的加速度，故 L di/dt 項中之電感 L 即相當於質量，與慣性有關（重從前章知此磁場一旦在空間中被建立，就不願平白無故消失，）。

 

LC 振盪的應用

收音機（原理見下）、電視的選台器。

關鍵是共振。

 

 

RLC （串列）電路

 

 

交流電

交流電動勢

使用交流電的主要好處是它可以透過變壓器改變電位差的大小，另一個好處則是交流電更適合發電機、馬達等轉動式電機機械的的運作方式，見圖，一個交流發電機：

E = Emax sin ωdt

其中 ωd 叫做驅動頻率。若此發電機是迴路的一部分，則將在迴路中造成一個正弦變化的電流

i = I sin (ωdt - φ)

注意這裏電流中多了相位，這是因為電流不一定跟電動勢同相位。

 

強迫振盪

 

 

三種負載電路

電阻性負載

E - vR = 0

移項

vR = Emax sin ωdt

對電阻，VR = Emax （振幅）

vR = VR sin ωdt

求電流，寫下電流滿足的方程式

iR = vR / R = VR/R sin ωdt

故電流可寫成

iR = I R sin ( ωdt - φ)

其中相位常數 φ = 0 ，且定義

VR = IR R

此關係可用之任何 AC 電路中之電阻，見圖。

 

電容性負載

如圖

vC = VC sin ωdt

其中 VC 是電容器兩端的電壓振幅，由電容的定義，此電壓來自

qC = C vC =C VC sin ωdt

求電流，找出電流滿足的方程式

iC = d qC / dt = ωd C VC cos ωdt

想把 iC 表示成標準形式以利比較

iC = I C sin ( ωdt - φ)

iC = (VC / XC) sin ( ωdt + 90.deg)

則須定義 "容抗" (capasitive reactance)

XC = 1/ ωd C

且電流之相位常數為 -90 度。

放故對電容之負載而言，電壓振幅與電流振幅的關係是：

V C = I C X C

見圖。

我們可以清楚看到，-90 度相位差來自於因為電流的積分才同步於驅動電動勢。

 

電感性負載

裝置如圖

感應電動勢來自驅動電動勢

vL = VL sin ωdt

而它與電流的關係是

vL = L diL / dt

故

diL / dt = VL/ L sin ωdt

diL = VL/ L sin(ωdt) dt

iL = ∫ diL = ∫ VL/ L sin(ωdt) dt = - (VL/ ωdL) cos(ωdt)

一樣為了表為標準形式

定義 "感抗" (inductive reactance)

XL = ωd L

得

iL = IL sin ( ωdt - φ)

φ= 90 deg

 

VL= IL XL

(compare V = I R, VC = IC RC)

見圖

 

RLC 串聯迴路

由於是串聯，因此流經各元件的電流都是同一個電流函數

i = I sin(ωdt - φ)

（請注意，若非如此，將導致淨電荷累積於迴路某處，即便是電容器也無法接受。）

我們要求的是電流值 i 與相位角 φ，本節用的是相位圖這種簡化的方法求解。

 

電流振幅

由迴路法則，電位需滿足

E = vR + vC +vL

 

把電壓（電動勢）用相量 (phasor) 表示出來，如圖 31-14，上式等號右邊是 (b) 圖、等號左邊是 (c) 圖。

vC 、 vL 先組合而得 (d) 圖，最後再用畢氏定理，得出關係

Emax2 = VR2 + (VL - VC)2 = I2 (R2 + (XL - XC)2)

表示為電流振幅，則為

I = Emax / √(R2 + (XL - XC)2)

定義 "阻抗" (impedance)

Z ≡ √( R2 + (XL - XC)2 )

則電流振幅為

I = Emax / Z

上式代入 XL 與 XC 的原定義值，各元件的特性量比較看得清楚：

I = Emax / √(R2 + (ωdL - 1/ωdC)2)

我們可以看到，I 的值是 ωdL 與 1/ωdC 的差距決是的。

以上描述的是接上交流電動勢後的穩定狀態（steady-state），當電動勢剛接上電路時，會產生一個暫態電流 (transient current)。此暫態時間是由 L/R 及 RC 兩個時間常數決定的。若未經仔細的計算與電路設計，暫態電流有可能會在電源一開動時毀壞一個馬達，比方說。

（譯本提到，暫態電流可能會非常大，為什麼？）

 

相位常數

從圖 31-14 (d) 可看出相位角 phi 具有以下關係

tanφ = ( VL - VC ) / VR = ( IXL - IXC ) / IR = ( XL - XC ) / R

這就是相位常數。

相位特性可以分為下面三種情形：

XL > XC：電感成份大於電容成分，相位角為正值。

XL < XC：電容成份大於電感成分，相位角為負值。

XL = XC：共振，此時相位角為零度。

 

共振

對給定的 R 值，最大電之振幅發生在

ωdL = 1/ωdC

即

ωd = 1/ √(L C)

其實 RLC 電路（R 不大者）的自然頻率是 1/ √(L C)，此即共振。

小 ωd 時，是感抗小、容抗大；大 ωd 時，是容抗小、感抗大。

共振曲線低頻的部分由容抗所支配，高頻的部分由感抗所支配（低頻電流有利充電，而高頻電流造成電磁感應大）。

 

RLC （串列）交流驅動電路 (公式美化版)

如何求解以下迴路？

普物的難度設定，使用 phaser Im 來描述 電流

前面已看到，交流電動勢的影響下，

電阻上的電流 i 與其跨元件電壓 VR 同相位

電容 上的電流 i 領先其跨元件電壓 VC 90 度

電感 上的電流 i 落後其跨元件電壓 VL 90 度

 

迴路上的電壓為之元件的總和（交流電動勢的影響已分別加諸在各別跨元件電壓上）

V = vR + vC + vL

由相位關係，視 V 為 phaser Vm 的投影，

有

Vm2 = VR2 + (VL - VC)2

而 VR、VL、 VC 從前面的結果，且同一（串列）迴路上電流只能相同，有

Vm2 = (Im R) 2 + (Im XL - Im XC)2

移項可解出 Im

由這裏定義出 impedance （阻抗）這個量，對決定此迴路上電流振幅大小是很有用的（也得到了簡化的圖像 Vm/Z）

 

接下來，繼續解電流的相位

討論

交流電路中的功率

RLC 電路中能量的來源是發電機，該能量一部分貯存於電容器的電場中，一部分貯存於電感器的磁場中，剩下的則在電阻器以熱能的方式消耗掉。。

P = i2 R = [I sin(ωdt - φ)]2 R

sin2 θ 的週期平均是 1/2

故

Pavg = 1/2 I2 R = (I/ √2)2 R

定 Irms = I/ √2

Pavg = Irms2 R

同法，可定

Vrms = V / √2 及 Erms = Emax / √2

現在，由於 Irms = I/ √2 且 Erms = Emax / √2 ，都差一樣的√2

我們也可以把之前建立的 I = Emax / Z 改寫為很常用的形式

Irms = Erms / Z

如此可得

Pavg = Irms Irms R = (Erms / Z) Irms R = Erms Irms (R/Z) = Erms Irms cosφ

以上是平均功率的公式，其中 cosφ 稱為功率因子 (power factor)。要達到輸能至電阻的最大功率，需使 cosφ 接近 1。

 

變壓器 (transformer)

變壓器除了變壓外，另一個應用是協助電動勢源與耗電能裝置之間達到阻抗匹配（何謂阻抗匹配？打沙包的例子），才提昇功率傳遞的效率（為什麼？）。

 

台電又被踢爆 黑心變壓器燒錢 2 億
http://www.libertytimes.com.tw/2012/new/may/5/today-fo1-2.htm

 

電力配送：能傳輸的需求

Pavg = E I

(7.35 × 105 V ) ( 500 A) = 368MW

Pavg = I2 R

(500 A)2 (220 Ω) = 55 MW

損耗約 15%

電壓降低成一半

(1000 A)2 (220 Ω) = 220 MW

己達 60% 的損耗

 

理想變壓器

基於用電的安全（低電壓）與降低傳輸的損耗（高電壓），我們需要使用變壓器來改變電位差。而保留 "電流×電壓" 的積是定值。（沒有直流的變壓器）

見圖 31-18，開關在 S ，線圈（有絕緣）繞在鐵芯上（鐵芯本身再片狀絕緣貼合，以減少渦電流）。

因為 E = - d(NΦB)/dt

所以 Eturn = E/N = - dΦB / dt

由於磁通量是相同的，因此主 (primary) 線圈與次 (secondary) 線圈的每匝電動勢是一樣的，

Eturn = Vp / Np = Vs / Ns

Vs = Vp (Ns/Np)

若匝數 Ns > Np ，則 Vs > Vp ，就叫升壓變壓器。

 

若開關 S 打開（斷路），則

迴路在開關 S 關上（通路）後會發生的事：

（見課本描述）

假設無能量損失，則發電機到主線圈的能量傳送率 Ip Vp 就會等於 Is Vs，因此有

Is = Ip Np / Ns

上式告訴我們，電流的轉換亦取決於匝數比。

出現在主電路的電流 Ip 是因為有電阻頁載 R 在副電路上，要找出 Ip ，由上式

Ip = Is Ns / Np

再拿 Is = Vs / R ，並且用上了前面已有之 Vs = Vp (Ns/Np)，則得

Ip = 1/R (Ns/Np)2 Vp =Vp / Req

其中 Req = (Np/Ns)2 R ，是主線路因副線路內有電阻負載而感受到的等效電阻。

 

阻抗匹配

若要讓電率勢最有效轉列電阻性負載上，則阻抗要匹配，即主、副線路阻抗相當。

太陽活動與輸電網路

見圖


美國草原大火延燒16公頃 揪出禍首竟是他們
http://news.ltn.com.tw/news/world/breakingnews/2175563

 

 

整流器

使用二極體

 

整流電路

如果在加上電容器，會讓電流的變化更穩定（更像直流電），叫做濾波。