電場與高斯定律

法拉第的電力線

法拉第是勤奮自學者，但未受正規教育，因此無法以向量微積分的數學寫下力或場的通式，但他自已構建了電力線（以及磁力線）的圖像（可由小指南針頭接尾一路畫出）。

法拉第的電力線圖像，可歸納出以下兩個規則陳述：

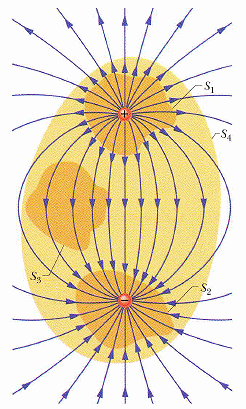
一、電力線出發自正電荷，終止於負電荷，中間不中斷。

二、電力線永不相交。

（補充：電荷越大，電力線越多）

 

另一個值得一提的補充：同向相鄰約電力線互相排擠開（異向則與鄰近電力線對消）。在後面的章節，我們將會看見這構成了 "場的能量密度"，的確與 "壓力" 有關。

 

 

電場

從（超距）力到場

場是空間的函數。引入場倒好處，是把超距力的機制局域化，也就是說，我們重新可以使用接觸的圖像（原本效應是隔著距離發生，現在則是由源先建構出場，而受力粒子再與它所在之處的場作用而感受到力）。

 

電場的定義

F = q E

或

F(r) = q E(r)

請注意，上式定義域的 r 是同一個 r ，它是受力電荷所在位置的 r ，從建立場的角度來講，有沒有那一顆受力電荷在，其實已經沒有關係。

E(r) = F(r) / q

 

點電荷造成的電場

r ≡ r_f - r_s

E(r) = Q / | r | ²  e_r

電偶極造成的電場

一正一負之點電荷加以整理，即得與距離三次方反比的公式：

利用電力線來數淨電荷

嚴謹的數學方法，見下

電通量

電力線會抵抗壓擠這個本性，暗示單位空間中的線數反映場的強度。基於力線是連續之故，可進一步看成單位面積通過的線數。此一強度可邊過 "電通量" 來數學化。

可利用單位面積

定義電通量，是電力

小面積元素可以定為向量，其大小是面積，方向是面的法向量：

 

Φ = E · A

 

高斯定律

Φ_CS =∫∫ E · dA = q / ε₀

 

高斯定律 與 庫倫定律

點電荷 庫倫定律 E = ( 1 / 4πε₀ ) ( q / r² )

 

一些特定對稱性下的例子

圓柱對稱

Φ_CS =∫∫ E · dA = E A = E (2πr L) = λ L / ε₀

故

E = λ/ ( 2πε₀ r )

 

平面對稱

 

 

球對稱

球殼

球殼外

 

球殼內

 

 

尖端（放電）與避雷針

電場方向與導體表面永遠垂直（否則分量會移動電荷使其重新分佈）

在越尖端處電場越強。

避雷針應該做成圓頭的較好（為什麼？見課本）

作業：解釋電漿球 (Plamsa Ball) 玩具的運作原理

http://en.wikipedia.org/wiki/Plasma_globe