物質的凝態：固體與流體

 

物質由原子構成

物質可以被無限分割嗎？還是有有最小單元？

 

原子論的復興

 

物質由原子構成的初期證據

晶體外形

X-Ray 繞射

 

物質的狀態：

物質的三相：固態、液態、氣態，有時會再加上電漿態（第四態）

沙子在微觀時像固體、巨觀時則像流體

課本中有再細分，連玻璃態與泡沫 (Foam) 和凝膠 (Gel) 都拿出來探討其不同。

 

拉張 (tension) 、壓縮 (compression) 與剪切 (shear)

固體的彈性

固體受外力的影響，在彈性限度  (elastic limit)

應力 (stress) = 彈性模量 (modulus of elasticity) × 應變 (strain)

 

應力 (stress) 與應變 (strain)

streach

F / A = Y ΔL / L

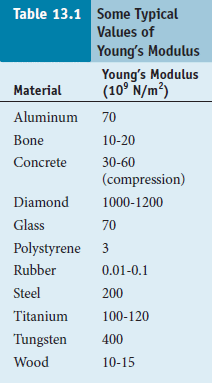
其中 Y 是楊氏模量

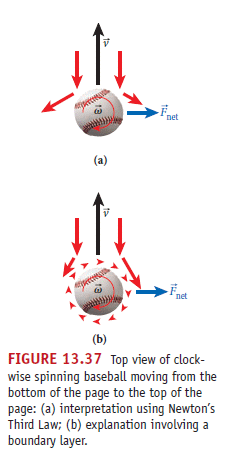
見圖 13.7

表 13.1 是常見值（鑽石最硬、鎢、鋼、鈦是金屬中較硬的，水泥的值則是加壓時適用，因為水泥不耐拉）

 

compress

F / A = B ΔV / V

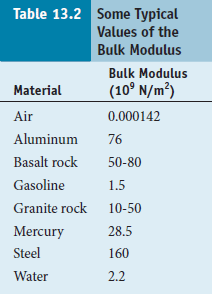
其中 B 是塊模量

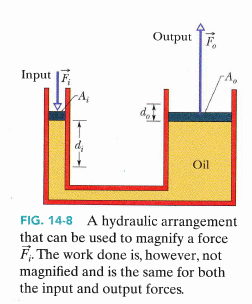
見圖 13.8

表 13.2 是常見值

 

shear

F / A = G ΔL / L

其中 G 是剪模量

見圖 13.9

表 13.3 是常見值

 

breaking stress

 

http://en.wikipedia.org/wiki/Ultimate_tensile_strength

http://www.kastenmarine.com/alumVSsteel.htm

http://www.brightspoke.com/c/understanding/bike-frame-materials.html

 

例題：

13.1 壁掛平面電視，求剪應力

SP 13.1 金屬線掛吊燈

 

 

 

壓力 (Pressure)（不是力，而是力除以面積）

本節考慮氣體與液體受外力的變化情形

p = F / A

 

壓力與深度的用關係

見課文推導（簡單）

p = p0 + ρ g h

壓力 = 液面氣壓 + 密度 × 重力加速度 × 深度

實驗證明見圖 13.14 （液面一樣高）

例題 13.2：潛水艇

 

氣壓計

見圖 13.16 水銀柱氣壓計

p0 = ρ g h

 

開管式氣壓計 圖 13.17

pg = p - p0 = ρ g h

 

氣體的氣壓與高度關係

前面推導深度與液壓關係時，把液體看成不可壓縮。氣體不適用此一假設，因此課本重新推導，見之

想緣像一薄層，上下兩面壓力差是該薄層重除以單位面積

Δp = - F / A = - mg / A = ρ V g  / A = ρ (Δh A) / A = - ρ g Δh

到目前為止與液壓並無不同，但氣維密麼與壓力呈成正比（在此當作理想氣體看），故有

p / p0 = ρ / ρ0

代入上式得

Δp / Δh =  - g ρ0 p / p0

當 Δh -> 0 時，則

dp / dh =  - (gρ0 / p0 )  p

積分得即 壓力與高度公式

p(h) = p0 exp [ - h g ρ0 / p0]

這個式子的準確度是相當不錯的，見圖 13. 18

例 13 .3 阿爾卑斯山的氣壓

 

帕斯卡原理

不可壓縮的流體，不允許系統內有壓力的不同，故該原理說

封閉容器內壓力之改變遍及整個液體

這一原理導致了油壓升降機之運用，見圖 13.21

 

阿基米德原理

故事：鑑定金王冠有沒有摻銀

 

浮力

想像靜止水中的一立方塊的，如圖 13.13，其中的一塊呈靜態平衡，因此浮力撐住自身的重量。是故，浮力大小取決於排開水之體積（細部導證見課文）

例題 13.4 冰山

密度不同之兩種不互溶液體的浮力實驗，見圖 13.25

 

 

物理玩具

浮力潛水艇、浮力潛水員 (Cartesian Diver)

http://fatlion.com/science/cartesian.html

http://en.wikipedia.org/wiki/Cartesian_diver

 

 

理想流體運動

Laminar flow

turbulent flow

incompressible flow

nonviscos flow

irrotational flow

 

伯努力方程式

是什麼提供飛機昇力，可做可樂罐吸管的實驗，見圖 13.31

推導 "連續方程式" ，假設理想流體，故不可壓縮

A1 v1 = A2 v2 （見圖 13.33）

從上式可得 體積流率 Rv = A v 及 質量流率 Rm = ρ A v

課本推導 13.1（分別從動能及位能作功，見圖 13.34）得

p1 + ρ g y1 + 1/2 ρ v12 =   p2 + ρ g y2 + 1/2 ρ v22

即

p + ρ g y + 1/2 ρ v2 = 常數

 

請特別注意：伯努力方程式的適用條件

理想流體，即無黏滯性、不可壓縮

 

在重力影響小的情況下

p + 1/2 ρ v2 = 常數

 

如此，可以解釋飲料罐吸管的實驗了

兩台大卡車高速首併駛應注意間距

賽車的設計要加強抓地力（設法讓底部流速高於頂部，或其他方法？）

問題：打排球時的上飄球跟下壓球各要怎麼打？

仔細討論

 

飛機（本段課文請務必細讀）

典型總重 3.4 MN，引擎總推力 0.9 MN

兩種極端圖像 Fig 13.36

不同飛行器及不同飛行階段

上翼面的增壓減壓效應也扮演重要角色，造成淨壓力下大於上

 

棒球的變化球作用機制

直接用伯努力的流速考量導致相反的結果

牛頓力學氣體撞擊的的圖像反而對

事實上，球拖著空氣走（避開考慮邊界的部分，才可套用伯努力方程式）

註：變化球的另一種個效應，旋球的尾氣流是偏轉的，故牛頓第三定律也有貢獻

網球殺球上切（上旋）及高爾夫球以下切來滯空時間 (4000 rpm)

高爾夫球上面的小凹孔是用來產生渦流以減少空氣阻力的，否則打不到 200 公尺遠

 

問題：為什麼流過機翼上面的空氣流速大？

http://www.allstar.fiu.edu/aero/airflylvl3.htm

http://www.regenpress.com/aerodynamics.pdf

http://www.straightdope.com/columns/read/2214/how-do-airplanes-fly-really

 

亦見：物理學飛行馬戲（中譯版第一冊）

 

一般流體的方程式：Navier - Stokes 方程式

因此需要用超級電腦來計算

 

例題 13.7 噴瓶口處的壓力差（假設流速 50m/s）

例題 SP  Venturi 管（用來推動陀螺儀）

 

放水

兩個桶容量相同，一個水位高、另一個水位低，挖一樣大小的洞，那桶水先流光？

伯努力方程式的應用，請自行見課本分析

例題 13.8 把瓶水放完需多久時間

 

 

黏滯性

黏滯係數

黏滯係數 = 單位面積的黏滯力 ／ 單位長度的速度差

η = ( F / A ) / ( Δv / h )

 

一個黏滯係數 是 η 的流體，在兩頭壓力差 Δp 下，其通過–個長 l 、半徑 r 的圓柱管其體積流率是

Rv = π r4 Δp / (8ηl )

 

典型的 黏滯係數 值

例題 13. 皮下注射針筒 (hypodermic needle) 進行注射時所需的推力（估計為 0.16 N）

但 0.16 N 約只為一支廉價原子筆的重量，事實上，注射之推力主要是為了克服密合活塞 (plunger) 與管壁的摩擦力。

 

 

亂流以及流體的尖端研究

決定紊流及層流之不同的主要關鍵，在於雷諾數

Re = ρ v L / η

雷諾數 Re 定出了流體內力與黏滯力間的比例（即內力比黏滯力大多少倍）（同時也代表系統總動量轉移比分子動量轉移大了多少倍的比率），小於 2000 產生層流，大於 4000 則紊流發生。

 

問題：為什麼可以用風洞及水池來模擬飛機及船舶與流體的交互作用？（雷諾數出現在那一個方程式中？）

對號不可壓縮的流體，若我們把 Navier-Stokes 方程式刻意整理成為全部都是無單位的變數（詳細的過程可見維基百科 http://en.wikipedia.org/wiki/Reynolds_number ），最後就會得出 雷諾數

重要結論：只要 Re 一樣，流體方程式的數學形式就相同

 

取自維基百科，圓柱通過流體產生的渦流

 

物理玩具

回力鏢 (Boomerrang)