轉動 (II)

轉動動能、轉動慣量、力矩

轉動動能：動能（平移、移動）與 轉動動能 的表示轉換

K = Σ (1/2) m_i v_i²

此時 v = ωr

K = Σ (1/2) m_i v_i² = Σ (1/2) m_i(ωr_i)² = (1/2) ω² [ Σm_i r_i² ]

定義 轉動慣量

I = Σm_i r_i²

則

K = (1/2) I ω²

這是 剛體 的 "轉動動能"，記得它完全可以由 (1/2) m v² 的基本形式得來。

 

 

轉動慣量

轉動慣量重要性

轉動慣量是代表轉動慣性的重要物理量

轉動慣量 的計算公式

I = Σm_i r_i²

對於連續體，則為

I = ∫r² dm

其中 dm 用 ρdv  也可以

一些常見均勻物體的轉動慣量，見表 H 10-2 或 B 10-1

注意參考表中，"軸" 的選取都通過質心，難到旋轉軸一定要通過質心？

不是，外力造成的轉動可以選任何軸。

所幸，不必每次重新計算轉動慣量，我們有平行軸定理

 

平行軸定理（再次提醒：定理是可證明的）

I = I_com + M h²

習題：證明平行軸定理（見課本）

 

一個剛體即便無外力（矩）下，也可以有多個（通過質心）轉動軸，這將會在角動量守恆單元來說明

 

力與力矩

再次由質點系統出發，從 F = ma 有 F_t = m a_t

定義力矩（及其等效表法）

τ= (r) (F sin (φ) ) = r F_t = (r sin(φ)) F

見課本圖 10-15 的圖解

牛頓第二定律的力矩形式

τ_net = I α

上式可以再次透過質點系統證明（以下的力是合力）

F_t = m a_t

同乘轉動半徑 r ，依力矩之定義

τ = r F_t = r m a_t

= r m (α r) = mr² α = I α

得證

功與轉動動能

我們之前有 功－動能定理，（課本複習 式 (10-49) ~ (10-51)）對於轉動而言（課本講 "假設這是物體唯一改變的能量"，

Δ K = K_f -K_i = W = ∫ τ d θ

由此可見，轉動作功為：

W = ∫ τ d θ

習題：證明 W = ∫ τ d θ

式 (10-52) ~ (10-55) 的證明見 (10-56) ~ (10-59)，大家要看習慣

等力矩特例下

W = τ(θ_f - θ_i)

平移與轉動的各相關公式對應

見課本表 H 10-3 或 B 10-1

例題

10-1 角位置與時間的關係

10-2 由角加速度求角速度與角位置

10-3 等角加速度的角度函數變化

10-4 減速過程求等角加速度

10-5 雲霄飛車頭痛症

10-6 轉動慣量

10-7 轉動慣量

10-8 轉動動能

10-9 滑輪

10-11 轉動動能

10-12 轉動運動方程式

 

習題

7

27

30

52

55

57

65

66

 

 

問題

待下一單元時一併討論

轉動 (III)

滾動、角動量 以及 其他形式的轉動

有摩擦力的轉動：滾動

輪子的發明

"Re-inventing the wheels" 是英文諺語，指聰明才智用在重覆前人己有之成果上，再偉大也是無用。

 

輪子的應用

把力轉向或導向

風車、水車

 

克服摩擦力

圓木墊在重物下拖、鋼珠軸承 (ball baring)

不一定要 "圓木" ，見： Curve of constant width

 

滾動的分析

接觸地的那一面是不滑動的

上沿速度是軸心速度的兩倍

s = θR

v_com = ωR

a_com = αR

 

 

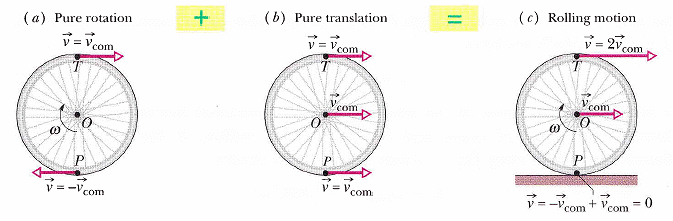
滾動動能

K = (1/2) I_p ω²

其中 p 是滾動軸心，即不動的那一點，如圖 H 11-4

I_p 大小不好算，但利用平行軸定理 I_p = I_com + M R² （其中 R 是車輪半徑），代入上式，得

K == (1/2) I_com ω² + (1/2) M R²ω² = (1/2) I_com ω² + (1/2) M v_com² =   K_rot 上述即為課本+ K_trans

上述即為課本 B (10.14) 式，可詮釋為： "滾動動能" = "質心動能" + "繞質心轉動動能"

 

平路上固定抓地力的加速問題

路平，不打滑（未達最大靜摩擦），輪子把地面向後推，地球質量太大無反應；而路面摩擦力施於輪子是一個向前的力，這個力與輪子對地面推力相反。因此輪子的加速度是向前。見課本圖 11-5 。問這個輪子怎庚運動。

分析：不打滑，故中心（質心）位置與轉動角位置具有固定的關係 s = θ R，也就是說質心速度與轉速同步 v_com = ω R，而質心加速度與角加速同步

a_com = α R

平順滾動 (smooth rolling) 具有以上的關係式

延伸難題：己知抓地力（即靜摩擦力）為 fs、輪子質量 M、轉動慣量 I，則 a_com 為多少？（那麼，這個問題要用 F = m a 還是 τ = α I ？施力下去，多少貢獻轉動？多少移動？可能的解法是？ ）（有制約條件的力學問題，用其他避免直接用牛頓運動定律的力學方法可能比較好解）

 

從斜坡上不打滑滾落的問題

見圖 11-6。 這是接續上面的結果。細部推導見課文。

 

溜溜球

課本說，這是一個行動實驗室。見課文。

質心動能 與 繞質心轉動動能

"剛體總動能" 可以分解成 "質心動能" 與 "繞質心轉動動能" ，這是一般性的結果。

作業（請助教演習課時提示）：上列陳述的證明。

力矩的應用

槓桿

給支點，撐起地球 -- 阿基米德 http://www.bud.org.tw/museum/s_star11.htm http://zh.wikipedia.org/zh-tw/阿基米德（那個時代就知逆地球是圓的嗎？）

作業：最早主張大地是圓的是誰？誰提出證明？

 

滑輪

見上一個單元（在課本中的例題有詳細示範）

再談力矩

τ = r × F

是三度空間中的表方法，最一般性的，注意這個力是作用於一點之上，見課本圖 H 11-8。

角動量與其守恆律

τ= 0 = r × F ，則 r × dp/dt = 0 ，也就是說 r × p 守恆，定角動量 l ≡ r × p

 

繞固定軸轉動之剛體的角動量

L = I ω

含動量與力的對照表：表 11-1

角動之守恆的應用

四種人物動作的例子

請見課文及圖

 

來福槍的子彈

空氣阻力 與 紊流（渦流）

http://fdrc.iit.edu/research/images/GridTurbulenceRe1.jpg

http://access.aasd.k12.wi.us/wp/baslerdale/files/2009/10/sphere-flow-comparison.jpg

來福線

來福 vs 滑膛

 

角動量玩具

溜溜球（課本己討論）

續進車 慣性車 (Friction Car or Inertia-wheel Car)（有飛輪）（不向後拉會向前衝的迴力車）

電光陀螺 (photo)

磁軸鐵軌飛輪 (photo)

竹蜻蜓

陀螺

扯鈴

倒立陀螺

http://home.phy.ntnu.edu.tw/~haha90/content/fun_exp/fun_content/top_back/top_back.html

 

陀螺儀 (Gyroscope)

用途：定方向

與指南針有什麼不同？

原理

示範與影片觀賞

操作示範

http://www.youtube.com/watch?v=8H98BgRzpOM&feature=channel

真的有用嗎？（轉子可以很重）

少見的應用

Gyrowheel
http://www.youtube.com/watch?v=Cbfe2_2DDc0&feature=player_embedded

從一輪看兩輪 http://www.youtube.com/watch?v=K4YmVP6i4qw&feature=related

 

討論：有些豪華遊艇上，也裝有陀螺儀，用來穩定船身減少搖晃，可能的作法為何？

陀螺穩定器：穩定船體的陀螺裝置。 20世紀初使用的施利克被動式穩定器實質上是一個裝在船上的大型二自由度重力陀螺儀，其轉子軸鉛直放置，框架軸平行於船的橫軸。當船體側搖時，陀螺力矩迫使框架攜帶轉子一起相對於船體旋進。這種搖擺式旋進引起另一個陀螺力矩，對船體產生穩定作用。斯佩里主動式穩定器是在上述裝置的基礎上增加一個小型操縱陀螺儀，其轉子沿船橫軸放置。一旦船體側傾，小陀螺沿其鉛直軸旋進，從而使主陀螺儀框架軸上的控制馬達及時開動，在該軸上施加與原陀螺力矩方向相同的主動力矩，藉以加強框架的旋進和由此旋進產生的對船體的穩定作用。(http://wiki.eworldship.com/index.php?doc-view-2531)

 

雙陀螺儀穩定器測試影片 (https://www.youtube.com/watch?v=3o4hzzItIxM)
(https://goo.gl/9VeJ3r)

 

其他形式的陀螺儀

微機電陀螺儀

iPhone 4 的新配備 http://www.ifixit.com/Teardown/iPhone-4-Gyroscope-Teardown/3156/1

光學陀螺儀

 

 

陀螺儀的進動

τ = dL/dt

dL = τ dt

其中 τ 的方向是 r × Fg，既要 ⊥ r，又要 ⊥ Fg

for L >> ΔL， 可見 L 的方向是沿著τ掃過的，如課本圖 11-21 所示

dL = Mgr dt

dφ = dL/L = Mgr/L dt = Mgr / Iω dt

dφ/dt = Mgr / Iω，這是進動角速度（又稱進動率）

上式 I 與 M 有關，故 進動率與 M 無關。

傅科擺 (Foucault pendulum)

因為地球自轉的關係，單擺的面會偏轉。

科氏力 (Coriolis force)（颱風與水槽旋渦的轉向、英德福克蘭附近海戰）

http://zh.wikipedia.org/zh-hk/科里奧利力

http://chenghm2008.pixnet.net/blog/post/22768109

 

史上最美的十項科學實驗，克里斯 （Robert P. Crease）http://blog.66wz.com/?uid-216821-action-viewspace-itemid-206402

◎(7) 地球的大小：埃拉托塞尼斯測度 地球的周長
◎(2) 自由落體：比薩斜塔的傳奇
◎(8) 阿爾法實驗：伽利略的斜面實驗
◎(4) 七彩光譜：牛頓的稜鏡分光實驗
◎(6) 幫地球量體重：卡文迪什嚴謹 的實驗
◎(5) 讓波發亮：楊氏簡單好懂的類比
◎(10) 地球的自轉：令人肅然起敬的傅科擺
◎(3) 漂移的電子：密立根的油滴實驗
◎(9) 晨曦之美：拉塞福發現了 原子核
◎(1) 唯一的謎團：單一電子的量子干涉實驗

 

作業：腳踏車只有一前一後兩個輪子為什麼不會側倒？

回應一：有無技術有差，真正厲害的一輪車也著到處跑。

回應二：跟行進狀態一定有關，放雙手的都是走動中的。

回應三：跟龍頭可轉一定有關，問任何何會騎的，不動龍頭豈不摔慘。

（網路上的參考資料 http://www.phy.ntnu.edu.tw/moodle/mod/resource/view.php?id=30）

 

表現物體轉動之慣性的量

轉動慣量（慣量矩）Moment of Inertia

換檔變速的目的

轉動座標系

轉動座標系 是不是一個慣性座標系？

判定方法，按定義 (1) 課本 "滿足牛頓定律的座標系" 稱之；(2)與實驗室座標系 差一相對速度的座標系。

 

為什麼要介紹或使用轉動座標系？

問題

無外力（矩）下轉量軸是否通過質心？

 

例題

11-2 球滾下斜坡

11-4 總角動量

11-7 角動量體驗玩具

11-8 轉盤角速率

習題

Temp

地球的質量如何測量？地球的重量如何測量？地心內部的壓力如何推估？