既然己經知道質心,看外力對質心的影響,透過推導(亦見Hailday 9-16)
![]()
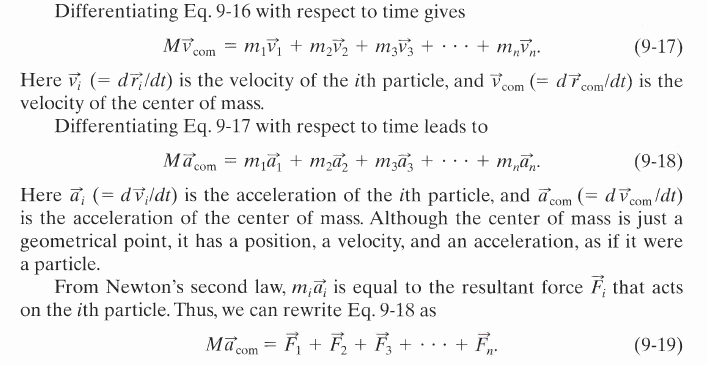
故重要的結論是
Fnet = M aCOM
很多的運動行為,可以簡化成看它的質心在動,而第二運動定律仍適用。
線動量守恆 與 碰撞
動量的定義 與 線動量守恆
之前曾提到尋找守恆量重要,在無外力的情況下,什麼不變?動量是守恆(不變)的。
直接來自牛頓第二運動定律 f = m a = m dv/dt = d(mv)/dt,如果我們定義 mv = P,叫作動量 (momentum) 也就是說,
f = dP/dt
(請注意這定義了動量與力之間的關係)
在無外力的情形下
dP/dt = 0
故我們有動量 P 不隨時間改變,(線)動量守恆。
在陸地上,快速行駛的沙石車之危險性,以及在海上,笨重的油輪一旦倒硨停船,都還要向前五公里才停得下來。這都是因為它們的動量很大。
質點系統的線動量守恆
動量在只有一個粒子時,重要性好像與速度差不多。但在質點系統裏(下一章會深入討論),它抓到了系統的重要特徵
P = Σi=1n pi = Σi=1n mi v i
因為是總動量守恆而不是總速度守恆。
質點系統的牛頓第二定律(下一章會深入討論)
既然己經知道質心,看外力對質心的影響,透過推導(亦見Hailday 9-16)
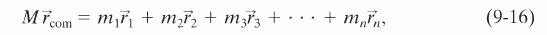
故重要的結論是
Fnet = M aCOM
很多的運動行為,可以簡化成看它的質心在動,而第二運動定律仍適用。
碰撞
兩個物體碰撞的過程及結果,可以是非常複雜,例如兩台車互撞。除了一團亂以外,這裏頭是否有一些規律性可言?
從另一個角度來看,撞球之間的碰撞簡單,高手的神乎其技的表演引人目光。所以碰撞僅乎是可以算得很精準的現象。
碰撞時,兩個物體交互作用的時間極短,我們因此另定一個方便的量來描述它們運動狀態的改變(其中最重要的兩種物體的運動狀態是位置(軌跡)及速度),即速度(乘上了質量後就之動量)的瞬間變化。我們之後會發現,動量比速度在描述運動上更有代表性,因此定義動量的瞬間改變。
碰撞的前後,動量守恆
動量守恆(無外力時)是前面己經證明的,只要是沒有外力,任何時刻動量都是守恆的。
pf1 + pf2 = pi1 + pi2
衝量(impulse)
處理極短時間內的動量改變,我們定義力對時間的積分為 衝量 ( impulse )
I ≡ ∫ F(t) dt = pf - pi
,基於此定義,衝量反映出動量改變,是碰撞前後最容易明確處理的量(碰撞過程的時間太短)。
衝量的單位是與動量是一樣的,為什麼還要定衝量?因為對於短瞬間的力作用過程,平均力,
Fave = I / Δt
更加有用,見圖 Bauer 7.3。
研究汽車撞擊測試的問題時,衝量就是一個重要的物理量了。(見課本圖 Bauer 7.6)安全氣囊,及潰縮機制都是為了延長作用時間(白話"緩衝")降低力人體受力的大小而設計的。
彈性碰撞 與 非彈性碰撞
彈性碰撞是碰撞前後能量守恆(為什麼彈性的碰撞就會這樣?因為彈性系統會把讓距離接近的質點的位能貯存起來,待遠離後再釋放乾淨,因此動能守恆)。例如:兩個撞球相撞。
至於非彈性碰撞,因為沒有還原交換成位能的動能(或者是一部分部分動能已變成位能),故動能不守恆。例如:兩車互撞卡在一起。
基本題型內藏了重要圖像,故務必閱讀演練。課文 7.4 節
彈道擺(衝擊擺)
測子彈的槍口速度
牛頓的搖籃 (Newton's Cradle)
作業:到 YouTube 用 Newton's Cradle 找影片,解釋所看到的現象。
利用動量守恆來找尋加速器實驗中之粒子
微中子的發現
頂夸克的存在(課本圖 Bauer 7.16)
對稱性與守恆量
動量守恆與慣性
之前我們提到,物體有慣性,而在本單元中闡明的 "無外力下動量守恆",則是物有 "慣性" 背後的基本理由。我們將會在後面的單元裏,再介紹角動量守恆以及與轉動有關的慣性量。
撞球、混沌、自由、自由/自主意識(free will),與拉卜拉斯精靈
見課文 Bauer 7.8 節
討論、例題 與 習題
討論
坐在椅子上腳不碰地仍能移動,怎麼辦到的?
一個人自己玩盪鞦韆,為何能一直盪而不被摩擦力消耗能量停止?
一手就可以把籃球拍起來開始運球,如何用物理解釋這個酷技?
例題
B 7.1 棒球
H 9-2 求質心
H 9-11 擺鎚球
習題
H Ch.9 第 17 、48 題