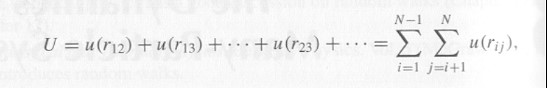
多粒子系統的(分子)動力學
分子動力學
要點:
牛頓運動方程式 f = ma ,f 是合力
由位勢求受力:粒子間的交互作用 (Lennard-Jones 位勢)
積分運動方程式:Verlet 演算法
週期性邊界條件 (減少表面效應)
巨觀 (熱力學) 量的計算:瞬間溫度、壓力
平衡
增減溫度的方法
牛頓運動方程式 f = ma ,f 是合力
由位勢求受力:粒子間的交互作用 (Lennard-Jones 位勢)
(註:Lennard-Jones 是一個人,不是兩個人的人各組合)
既然位能是兩個粒子距離的函數,則子的受力也會是距離的函數,大小相等,方向相反。
將上列 Lennard-Johns 位勢函數,對受力粒子的位置座標 (偏) 微分,會得到粒子受力,形式如下:
積分運動方程式:Verlet 演算法
週期性邊界條件 (減少表面效應)
暖身練習:單球反射壁彈回動畫
範例程式:(1) 留下軌跡不清除 particle_in_box.f
範例程式:(2) 清除軌跡成為動畫 particle_in_box_animate.f
暖身練習:單球週期性邊界條件
將上面反射壁動畫改為使用週期性邊界條件。 範例程式: particle_in_box_PBC.f
暖身練習:將單球擴展為雙球
改寫單球反射璧版本,使成為雙球,使用陣列。範例程式: two_particles_in_box_animate.f
暖身練習:替雙球系統加入交互作用
加入 Lennard-Jones 位勢的力場(尚末將運算效率最佳化) : two_particles_LJ.f
以成對方式處理作用力(提昇效率),並將壁反射移入副程式:two_particles_LJ_pair.f
進階練習:再改為週期性邊界條件
擴充至 n 個粒子,並且改為用週期性邊界條件(並注使用 二維 3X3=9 個、三維 3X3X3=27 個 cell 的技術來獲得任兩個粒子間的距離) : n_particles_LJ_PBC.f
不使用 Verlect Algorithm : n_particles_LJ_PBC_no-verlect.f
使用 Verlect Algorithm : n_particles_LJ_PBC_verlect.f
進階練習:使用亂數
使用方法:call random_number(r)
,會在 r 內填入 0.0 至 1.0 之間的實數值
使用亂數產生器來初始化位置與速度:n_particles_LJ_PBC_rand_dis.f
單位的選取
單位的選取上,儘量使需要處理的量保持在不過大或過小,否則會浪費電腦的有效精確位數。
巨觀 (熱力學) 量的計算:瞬間溫度、壓力
瞬間溫度的定義,是基於系統動能
壓力
理想氣體的話,瞬間壓力是 Pideal = NkT / V
有碰撞者,則要進一步考慮
平均壓力 P ≡ < P(t) > ,在程式中要計算的量是
叫作 virial ,代表對理想氣體的粒子交互作用修正。
進階練習:加入溫度與壓力
平衡
對於多體系統而言,平衡是用在巨觀世界的觀念,它描述那個多體系統的某個量,在一定的時間區間內作平均的值如果長時間都不再改變,則這個量己經達到平衡。例如密度這個量,從微觀的角度看,某個區域的瞬間密度由該區域內的粒子數來決定,然而粒子隨時進出數目不斷在變,只是一段時間內的平均密度仍維持定值。
範例程式 md_pgplot.f 執行檔 md_pgplot.x
原課本習題:p.227、p.229、p.231、p.233、p.235、p.237
助教翻譯之 習題 8-1 ~ 8-10 (中文)
增減溫度的方法
溫度完全就是由動能決定,而動能又取決於質點運動的速率。因此瞬間速率的人為放大或縮小即是升降溫度。
範例程式:升降溫循環,可觀察到三態的變化